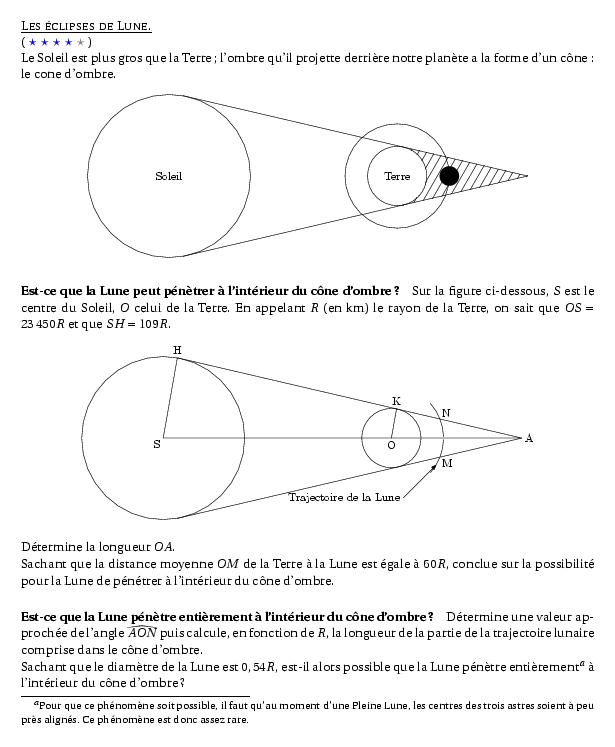
%@metapost:3cumulexo25.mp %@Titre: Les éclipses de Lune. %@Dif:4 \begin{minipage}{\linewidth} Le Soleil est plus gros que la Terre; l'ombre qu'il projette derrière notre planète a la forme d'un cône : le cone d'ombre. \[\includegraphics{3cumulexo25.2}\] \paragraph{Est-ce que la Lune peut pénètrer à l'intérieur du cône d'ombre ?} Sur la figure ci-dessous, $S$ est le centre du Soleil, $O$ celui de la Terre. En appelant $R$ (en km) le rayon de la Terre, on sait que $OS=23\,450R$ et que $SH=109R$. \[\includegraphics{3cumulexo25.1}\] Détermine la longueur $OA$. \par Sachant que la distance moyenne $OM$ de la Terre à la Lune est égale à $60R$, conclue sur la possibilité pour la Lune de pénétrer à l'intérieur du cône d'ombre. \paragraph{Est-ce que la Lune pénètre entièrement à l'intérieur du cône d'ombre ?} Détermine une valeur approchée de l'angle $\widehat{AON}$ puis calcule, en fonction de $R$, la longueur de la partie de la trajectoire lunaire comprise dans le cône d'ombre. \par Sachant que le diamètre de la Lune est $0,54R$, est-il alors possible que la Lune pénètre entièrement\footnote{Pour que ce phénomène soit possible, il faut qu'au moment d'une Pleine Lune, les centres des trois astres soient à peu près alignés. Ce phénomène est donc assez rare.} à l'intérieur du cône d'ombre ? \end{minipage}