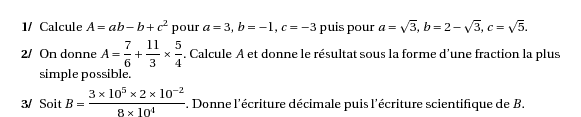
%@P:exocorcp \begin{myenumerate} \item Calcule $A=ab-b+c^2$ pour $a=3$, $b=-1$, $c=-3$ puis pour $a=\sqrt3$, $b=2-\sqrt3$, $c=\sqrt5$. \item On donne $A=\dfrac76+\dfrac{11}3\times\dfrac54$. Calcule $A$ et donne le résultat sous la forme d'une fraction la plus simple possible. \item Soit $B=\dfrac{3\times10^5\times2\times10^{-2}}{8\times10^4}$. Donne l'écriture décimale puis l'écriture scientifique de $B$. \end{myenumerate} %@Correction: \begin{myenumerate} \item On trouve $A=7$ puis \[\Eqalign{ A&=\sqrt3(2-\sqrt3)-(2-\sqrt3)+\left(\sqrt5\right)^2\cr A&=2\sqrt3-3-2+\sqrt3+5\cr A&=2\cr }\] \item \[\Eqalign{ A&=\frac76+\frac{11}3\times\frac54\kern0.1\linewidth&B&=\frac{3\times10^5\times2\times10^{-2}}{8\times10^4}\cr A&=\frac76+\frac{55}{12}&B&=\frac{3\times2\times10^5\times10^{-2}}{8\times10^4}\cr A&=\frac{14}{12}+\frac{55}{12}&B&=\frac{6\times10^3}{8\times10^4}\cr A&=\frac{69}{12}&B&=\frac68\times\frac{10^3}{10^4}\cr A&=\frac{23}4&B&=0,75\times10^{-1}\cr &&B&=0,075\mbox{ \'Ecriture décimale}\cr &&B&=7,5\times10^{-2}\mbox{ \'Ecriture scientifique}\cr }\] \end{myenumerate}