exo6.tex

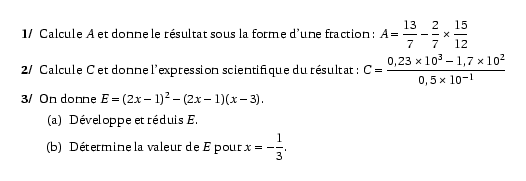
%@P:exocorcp
\begin{myenumerate}
\item Calcule $A$ et donne le résultat sous la forme d'une fraction :
$A=\dfrac{13}7-\dfrac27\times\dfrac{15}{12}$
\item Calcule $C$ et donne l'expression scientifique du résultat : %
$C=\dfrac{0,23\times10^3-1,7\times10^2}{0,5\times10^{-1}}$
\item On donne $E=(2x-1)^2-(2x-1)(x-3)$.
\begin{enumerate}
\item Développe et réduis $E$.
\item Détermine la valeur de $E$ pour $x=-\dfrac13$.
\end{enumerate}
\end{myenumerate}
%@Correction:
\begin{myenumerate}
  \item\[\Eqalign{
A&=\frac{13}7-\frac27\times\frac{15}{12}\cr
A&=\frac{13}7-\frac{2\times15}{7\times6\times2}\cr
A&=\frac{13}7-\frac{15}{42}\cr
A&=\frac{78}{42}-\frac{15}{42}\cr
A&=\frac{63}{42}\cr
A&=\frac32\cr
}\]
\item \[\Eqalign{
C&=\frac{0,23\times10^3-1,7\times10^2}{0,5\times10^{-1}}\cr
C&=\frac{230-170}{0,05}\cr
C&=\frac{60}{0,05}\cr
C&=1\,200\cr
C&=1,2\times10^3\cr
}\]
\item
  \begin{enumerate}
  \item \[\Eqalign{
E&=(2x-1)^2-(2x-1)(x-3)\cr
E&=(2x)^2-2\times2x\times1+1^2-\left(2x\times x-2x\times3-1\times
  x-1\times(-3)\right)\cr
E&=4x^2-4x+1-\left(2x^2-6x-x+3\right)\cr
E&=4x^2-4x+1-\left(2x^2-7x+3\right)\cr
E&=4x^2-4x+1-2x^2+7x-3\cr
E&=2x^2+3x-2\cr
}\]
\item \[\Eqalign{
E&=2x^2+3x-2\cr
E&=2\times\left(-\frac13\right)^2+3\times\left(-\frac13\right)-2\cr
E&=2\times\left(\frac19\right)-1-2\cr
E&=\frac29-3\cr
E&=\frac29-\frac{27}9\cr
E&=-\frac{25}9\cr
}\]
  \end{enumerate}
\end{myenumerate}