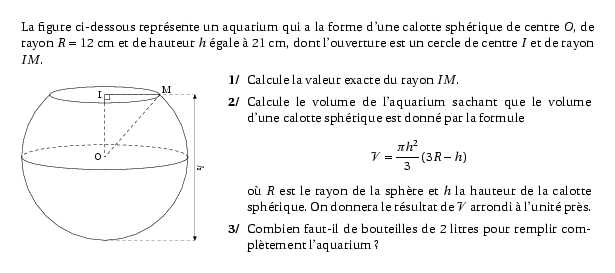
%@metapost: 302dm06.mp La figure ci-dessous représente un aquarium qui a la forme d'une calotte sphérique de centre $O$, de rayon $R=12$~cm et de hauteur $h$ égale à 21~cm, dont l'ouverture est un cercle de centre $I$ et de rayon $IM$. \par\vspace{3mm} \compo{2}{302dm06}{0.85}{ \begin{myenumerate} \item Calcule la valeur exacte du rayon $IM$. \item Calcule le volume de l'aquarium sachant que le volume d'une calotte sphérique est donné par la formule \[{\cal V}=\frac{\pi h^2}3\left(3R-h\right)\] où $R$ est le rayon de la sphère et $h$ la hauteur de la calotte sphérique. On donnera le résultat de ${\cal V}$ arrondi à l'unité près. \item Combien faut-il de bouteilles de 2 litres pour remplir complètement l'aquarium ? \end{myenumerate} }