exo28.tex

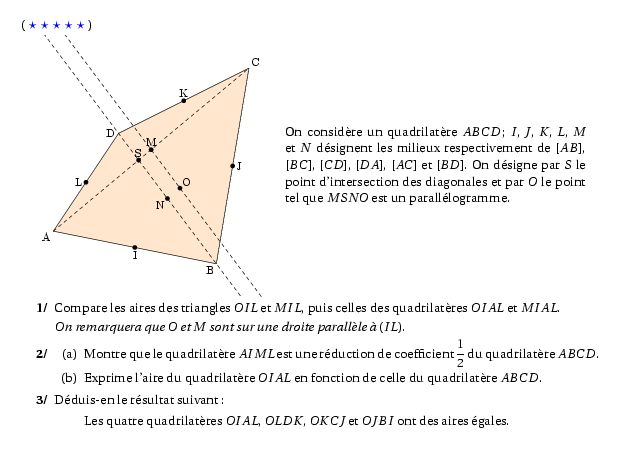
%@metapost:3geoplaneexo28.mp
%@Dif:5
\par\compo{1}{3geoplaneexo28}{1}{On considère un quadrilatère $ABCD$; $I$, $J$, $K$, $L$, $M$ et $N$ désignent les milieux respectivement de $[AB]$, $[BC]$, $[CD]$, $[DA]$, $[AC]$ et $[BD]$. On désigne par $S$ le point d'intersection des diagonales et par $O$ le point tel que $MSNO$ est un parallélogramme.
}
\begin{myenumerate}
  \item Compare les aires des triangles $OIL$ et $MIL$, puis celles des quadrilatères $OIAL$ et $MIAL$.
\par{\em On remarquera que $O$ et $M$ sont sur une droite parallèle à $(IL)$.}
  \item
    \begin{enumerate}
      \item Montre que le quadrilatère $AIML$ est une réduction de coefficient $\dfrac12$ du quadrilatère $ABCD$.
      \item Exprime l'aire du quadrilatère $OIAL$ en fonction de celle du quadrilatère $ABCD$.
    \end{enumerate}
  \item Déduis-en le résultat suivant :
    \begin{quote}
      Les quatre quadrilatères $OIAL$, $OLDK$, $OKCJ$ et $OJBI$ ont des aires égales.
    \end{quote}
\end{myenumerate}