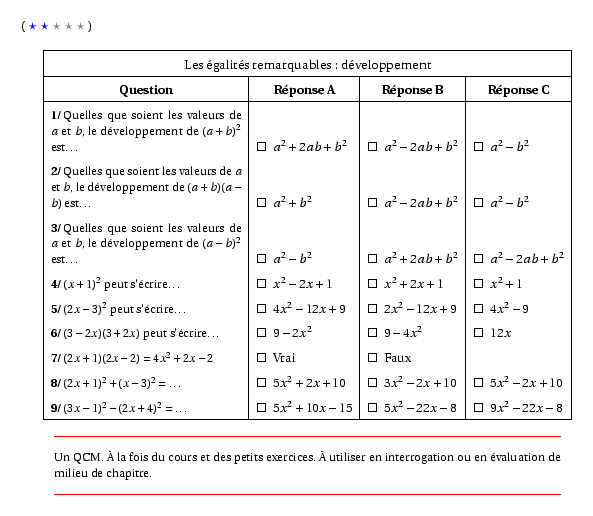
%@P:exocorcp %@Dif:2 \begin{center} \begin{Qcm}[3] \multicolumn{4}{|c|}{Les égalités remarquables : développement}\\ \hline \multicolumn{1}{|c|}{\bf Question}&\multicolumn{1}{c|}{\bf Réponse A}&\multicolumn{1}{c|}{\bf Réponse B}&\multicolumn{1}{c|}{\bf Réponse C}\\ \hline Quelles que soient les valeurs de $a$ et $b$, le développement de $(a+b)^2$ est\ldots&\V{$a^2+2ab+b^2$}&\F{$a^2-2ab+b^2$}&\F{$a^2-b^2$}\\ Quelles que soient les valeurs de $a$ et $b$, le développement de $(a+b)(a-b)$ est\ldots&\F{$a^2+b^2$}&\F{$a^2-2ab+b^2$}&\V{$a^2-b^2$}\\ Quelles que soient les valeurs de $a$ et $b$, le développement de $(a-b)^2$ est\ldots&\F{$a^2-b^2$}&\F{$a^2+2ab+b^2$}&\V{$a^2-2ab+b^2$}\\ $(x+1)^2$ peut s'écrire\ldots&\F{$x^2-2x+1$}&\V{$x^2+2x+1$}&\F{$x^2+1$}\\ $(2x-3)^2$ peut s'écrire\ldots&\V{$4x^2-12x+9$}&\F{$2x^2-12x+9$}&\F{$4x^2-9$}\\ $(3-2x)(3+2x)$ peut s'é\-cri\-re\ldots&\F{$9-2x^2$}&\V{$9-4x^2$}&\F{$12x$}\\ $(2x+1)(2x-2)=4x^2+2x-2$&\F{Vrai}&\V{Faux}&\\ $(2x+1)^2+(x-3)^2=\ldots$&\F{$5x^2+2x+10$}&\F{$3x^2-2x+10$}&\V{$5x^2-2x+10$}\\ $(3x-1)^2-(2x+4)^2=\ldots$&\F{$5x^2+10x-15$}&\V{$5x^2-22x-8$}&\F{$9x^2-22x-8$}\\ \end{Qcm} \end{center} %@Correction: \begin{center} \begin{Qcmcor}[3] \multicolumn{4}{|c|}{Les égalités remarquables : développement}\\ \hline \multicolumn{1}{|c|}{\bf Question}&\multicolumn{1}{c|}{\bf Réponse A}&\multicolumn{1}{c|}{\bf Réponse B}&\multicolumn{1}{c|}{\bf Réponse C}\\ \hline Quelles que soient les valeurs de $a$ et $b$, le développement de $(a+b)^2$ est\ldots&\V{$a^2+2ab+b^2$}&\F{$a^2-2ab+b^2$}&\F{$a^2-b^2$}\\ Quelles que soient les valeurs de $a$ et $b$, le développement de $(a+b)(a-b)$ est\ldots&\F{$a^2+b^2$}&\F{$a^2-2ab+b^2$}&\V{$a^2-b^2$}\\ Quelles que soient les valeurs de $a$ et $b$, le développement de $(a-b)^2$ est\ldots&\F{$a^2-b^2$}&\F{$a^2+2ab+b^2$}&\V{$a^2-2ab+b^2$}\\ $(x+1)^2$ peut s'écrire\ldots&\F{$x^2-2x+1$}&\V{$x^2+2x+1$}&\F{$x^2+1$}\\ $(2x-3)^2$ peut s'écrire\ldots&\V{$4x^2-12x+9$}&\F{$2x^2-12x+9$}&\F{$4x^2-9$}\\ $(3-2x)(3+2x)$ peut s'é\-cri\-re\ldots&\F{$9-2x^2$}&\V{$9-4x^2$}&\F{$12x$}\\ $(2x+1)(2x-2)=4x^2+2x-2$&\F{Vrai}&\V{Faux}&\\ $(2x+1)^2+(x-3)^2=\ldots$&\F{$5x^2+2x+10$}&\F{$3x^2-2x+10$}&\V{$5x^2-2x+10$}\\ $(3x-1)^2-(2x+4)^2=\ldots$&\F{$5x^2+10x-15$}&\V{$5x^2-22x-8$}&\F{$9x^2-22x-8$}\\ \end{Qcmcor} \end{center} %@Commentaire: Un QCM. \`A la fois du cours et des petits exercices. \`A utiliser en interrogation ou en évaluation de milieu de chapitre.