exo20.tex

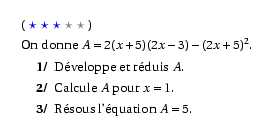
%@P:exocorcp
%@Dif:3
On donne $A=2(x+5)(2x-3)-(2x+5)^2$.
\begin{myenumerate}
\item Développe et réduis $A$.
\item Calcule $A$ pour $x=1$.
\item Résous l'équation $A=5$.
\end{myenumerate}
%@Correction:
\begin{myenumerate}
  \item\[\Eqalign{
A&=2(x+5)(2x-3)-(2x+5)^2\cr
A&=2(2x^2-3x+10x-15)-((2x)^2+2\times2x\times5+5^2)\cr
A&=4x^2-6x+20x-30-(4x^2+20x+25)\cr
A&=4x^2+14x-30-4x^2-20x-25\cr
A&=-6x-55\cr
}\]
\item Pour $x=1$, on a $A=-6\times1-55=-61$.
\item \[\Eqalign{
A&=5\cr
-6x-55&=5\cr
-6x&=60\cr
x&=-10\cr
}\]
La solution de l'équation est $x=-10$.
\end{myenumerate}