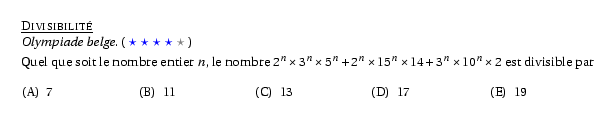
%@P:exocorcp %@Titre:Divisibilité %@Auteur: Olympiade belge. %@Dif:4 Quel que soit le nombre entier $n$, le nombre $2^n\times3^n\times5^n+2^n\times15^n\times14+3^n\times10^n\times2$ est divisible par \begin{multicols}{5} \begin{enumerate}[(A)] \item 7 \item 11 \item 13 \item 17 \item 19 \end{enumerate} \end{multicols} %@Correction: \[\Eqalign{ A&=2^n\times3^n\times5^n+2^n\times15^n\times14+3^n\times10^n\times2\cr A&=2^n\times3^n\times5^n+2^n\times(5\times3)^n\times14+3^n\times(2\times5)^n\times2\cr A&=2^n\times3^n\times5^n+2^n\times5^n\times3^n\times14+3^n\times2^n\times5^n\times2\cr A&=\underline{2^n3^n5^n}+\underline{2^n3^n5^n}\times14+\underline{2^n3^n5^n}\times2\cr A&=\underline{2^n3^n5^n}\times(1+14+2)\cr A&=\underline{2^n3^n5^n}\times17\cr }\] Il est donc divisible par 17.