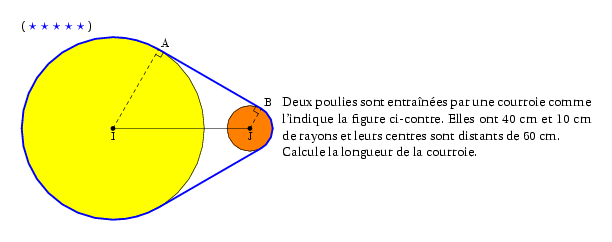
%@P:exocorcp %@metapost:pbgeo304exo01.mp %@Dif:5 \par\compo{1}{pbgeo304exo01}{1}{Deux poulies sont entraînées par une courroie comme l'indique la figure ci-contre. Elles ont 40~cm et 10~cm de rayons et leurs centres sont distants de 60~cm. \\Calcule la longueur de la courroie. } %@Correction: \par\compo{2}{pbgeo304exo01}{1}{\paragraph{\'Etape \no1} Complétons la figure. \paragraph{\'Etape \no2} Les droites $(IA)$ et $(JB)$ sont toutes deux perpendiculaires à la droite $(AB)$ donc les droites $(IA)$ et $(JB)$ sont parallèles. Elles définissent donc des angles $\widehat{AIJ}$ et $\widehat{BJO}$ correspondants égaux. } \paragraph{\'Etape \no3} On exprime $\cos\widehat{AIJ}$ et $\cos\widehat{BJO}$ pour obtenir \[\frac{IA}{IO}=\frac{JB}{JO}\mbox{ ou }\frac{40}{60+JO}=\frac{10}{JO}\] ce qui donne $JO=20$. \paragraph{\'Etape \no4} On détermine les angles $\widehat{BJO}$ et $\widehat{AIJ}$, tous deux égaux à 60\degres.\\On détermine ensuite la longueur de la courroie sur la petite poulie : \[2\times\dfrac{2\times\pi\times10\times60}{360}\] \\On détermine ensuite la longueur de la courroie sur la grande poulie : \[2\times\dfrac{2\times\pi\times40\times120}{360}\] \\On détermine ensuite la longueur $AB$ à l'aide du théorème de Pythagore : \[AB=\sqrt{80^2-40^2}-\sqrt{20^2-10^2}\] \paragraph{\'Etape \no5} On calcule la longueur $\mathscr{L}$ de la poulie \[\mathscr{L}\approx292,4~\mbox{cm}\]