exo23.tex

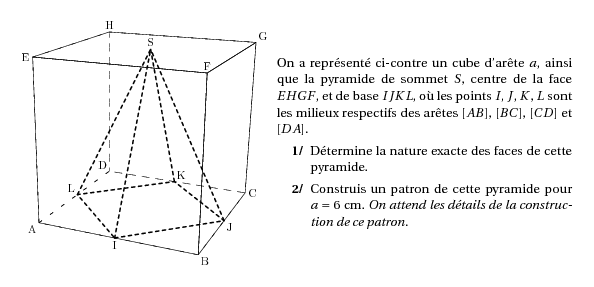
%@P:exocorcp
%@metapost:3problemegeoexo23.mp
\compo{1}{3problemegeoexo23}{1}{On a représenté ci-contre un cube d'arête
  $a$, ainsi que la pyramide de sommet $S$, centre de la face $EHGF$,
  et de base $IJKL$, où les points $I$, $J$, $K$, $L$ sont les milieux
  respectifs des arêtes $[AB]$, $[BC]$, $[CD]$ et $[DA]$.
\begin{myenumerate}
  \item Détermine la nature exacte des faces de cette pyramide.
  \item Construis un patron de cette pyramide pour $a=6$~cm. {\em On
      attend les détails de la construction de ce patron.}
\end{myenumerate}}
%@Correction:
\begin{myenumerate}
  \item Toutes les faces latérales sont des triangles isocèles en
    $S$.\par
    D'après le théorème des milieux appliqué deux fois, on démontre
    que les droites $(IJ)$ et $(KL)$ sont parallèles ainsi que
    $IJ=KL$.
    \\De même, on démontre que les droites $(LI)$ et $(JK)$ sont
    parallèles et $LI=JK$.
    \\$IJKL$ est un losange.
    \par De plus, les triangles $DKL$ et $JCK$ sont rectangles
    isocèles. Cela prouve que $\widehat{JKL}$ est un angle droit.\\Par
    conséquent, $IJKL$ est un carré.
  \item On trace le carré $ABCD$ pour construire la base $IJKL$. La
    longueur $IS$ est la la longueur de l'hypoténuse du triangle
    rectangle $IOS$ où $O$ est le centre de la face $ABCD$; ces
    dimensions sont $IO=3$~cm et $SO=6$~cm. Donc $IS=ID$. D'où la construction
    ci-dessous.
    \[\includegraphics{3problemegeoexo23.2}\]
\end{myenumerate}