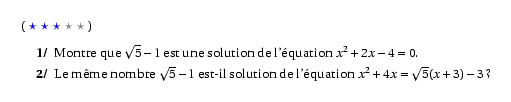
%@P:exocorcp %@Dif:3 \begin{myenumerate} \item Montre que $\sqrt5-1$ est une solution de l'équation $x^2+2x-4=0$. \item Le même nombre $\sqrt5-1$ est-il solution de l'équation $x^2+4x=\sqrt5(x+3)-3$ ? \end{myenumerate} %@Correction: \begin{myenumerate} \item \[\Eqalign{ \left(\sqrt5-1\right)^2+2\times\left(\sqrt5-1\right)-4\cr \sqrt5^2-2\times\sqrt5\times1+1^2+2\sqrt5-2-4\cr 5-2\sqrt5+1+2\sqrt5-2-4\cr 0\cr }\] Donc $\sqrt5-1$ est bien solution de l'équation $x^2+2x-4=0$. \item \[\Eqalign{ \left(\sqrt5-1\right)^2+4\left(\sqrt5-1\right)\kern2cm&&\sqrt5\times(\sqrt5-1+3)-3\cr 5-2\sqrt5+1+4\sqrt5-4&&\sqrt5(\sqrt5+2)-3\cr 2+2\sqrt5&&5+2\sqrt5-3\cr &&2+2\sqrt5 }\] Donc $\sqrt5-1$ est aussi solution de l'équation $x^2+4x=\sqrt5(x+3)-3$. \end{myenumerate} %@commentaire: Calculs sur les racines carrées dans un autre contexte. Réinvestissement du vocabulaire des {\em équations}.