exo58.tex

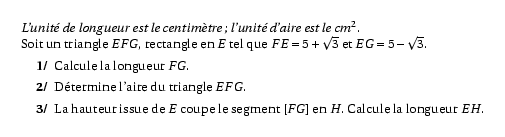
%@P:exocorcp
{\em L'unité de longueur est le centimètre; l'unité d'aire est le
  cm$^2$}.\par Soit un triangle $EFG$, rectangle en $E$ tel que
$FE=5+\sqrt3$ et $EG=5-\sqrt3$.
\begin{myenumerate}
  \item Calcule la longueur $FG$.
  \item Détermine l'aire du triangle $EFG$.
  \item La hauteur issue de $E$ coupe le segment $[FG]$ en
    $H$. Calcule la longueur $EH$.
\end{myenumerate}
%@Correction:
\begin{myenumerate}
  \item Dans le triangle $EFG$, rectangle en $E$, le théorème de
    Pythagore permet d'écrire :
    \[\Eqalign{
      FG^2&=FE^2+EG^2\cr
      FG^2&=\left(5+\sqrt3\right)^2+\left(5-\sqrt3\right)^2\cr
      FG^2&=5^2+2\times5\times\sqrt3+\sqrt3^2+5^2-2\times5\times\sqrt3+\sqrt3^2\cr
      FG^2&=25+10\sqrt3+3+25-10\sqrt3+3\cr
      FG^2&=59\cr
      FG&=\sqrt{59}\cr
    }\]
  \item
    \[\Eqalign{
      \mathscr A_{EFG}&=\frac{EF\times EG}2\cr
      \mathscr
      A_{EFG}&=\frac{\left(5+\sqrt3\right)\times\left(5-\sqrt3\right)}2\cr
      \mathscr A_{EFG}&=\frac{5^2-\sqrt3^2}2\cr
      \mathscr A_{EFG}&=\frac{25-3}2\cr
      \mathscr A_{EFG}&=11~\mbox{cm}^2\cr
    }\]
  \item
    \[\Eqalign{
      \mathscr A_{EFG}&=\frac{FG\times EH}2\cr
      11&=\frac{\sqrt{59}\times EH}2\cr
      22&=\sqrt{59}\times EH\cr
      \frac{22}{\sqrt{59}}&=EH\cr
    }\]
\end{myenumerate}