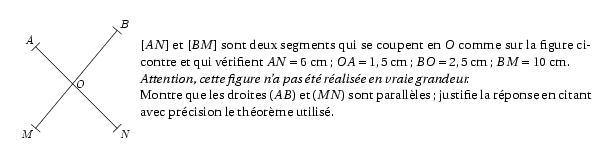
%@P:exocorcp %@metapost: 301ds04.mp \par\compo{1}{301ds04}{1}{$[AN]$ et $[BM]$ sont deux segments qui se coupent en $O$ comme sur la figure ci-contre et qui vérifient $AN=6$~cm; $OA=1,5$~cm; $BO=2,5$~cm; $BM=10$~cm. \par{\em Attention, cette figure n'a pas été réalisée en vraie grandeur.} \par Montre que les droites $(AB)$ et $(MN)$ sont parallèles ; justifie la réponse en citant avec précision le théorème utilisé. } %@Correction: Dans le triangle $AOB$, le point $N$ appartient à la droite $(AO)$ et le point $M$ appartient à la droite $(OB)$. \[\left. \begin{array}{l} \dfrac{OA}{ON}=\dfrac{1,5}{4,5}=\dfrac{15}{45}=\dfrac13\\ \\ \dfrac{OB}{OM}=\dfrac{2,5}{7,5}=\dfrac{25}{75}=\dfrac13\\ \end{array} \right\}\frac{OA}{ON}=\frac{OB}{OM}\] De plus, les points $O$, $A$, $N$ sont alignés dans le même ordre que les points $O$, $B$, $M$. Donc les droites $(AB)$ et $(MN)$ sont parallèles d'après la réciproque du théorème de Thalès.