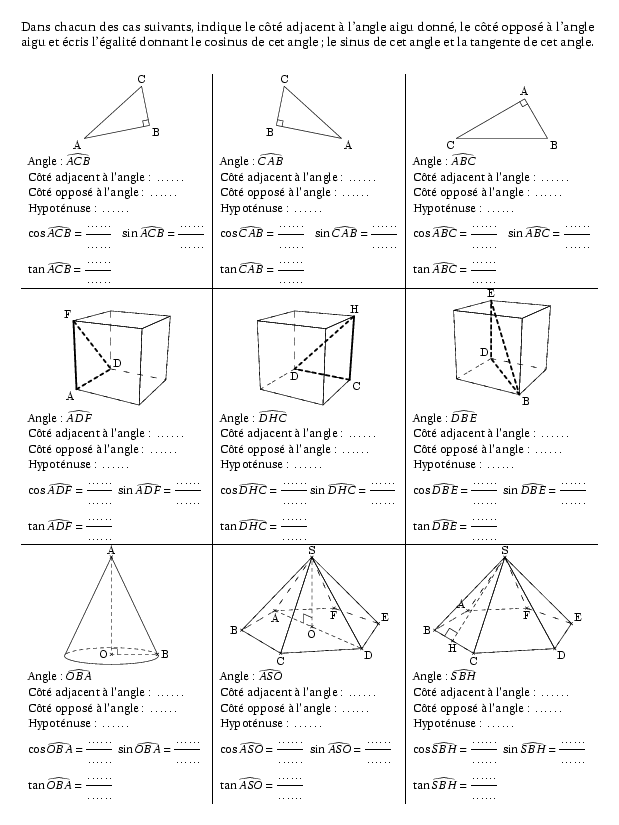
%@metapost:3trigoexo36.mp Dans chacun des cas suivants, indique le côté adjacent à l'angle aigu donné, le côté opposé à l'angle aigu et écris l'égalité donnant le cosinus de cet angle; le sinus de cet angle et la tangente de cet angle. {\small \begin{center} \begin{tabular}{l|l|l} \multicolumn{1}{c|}{\includegraphics{3trigoexo36.1}}&\multicolumn{1}{c|}{\includegraphics{3trigoexo36.2}}&\multicolumn{1}{c}{\includegraphics{3trigoexo36.3}}\\ Angle : $\widehat{ACB}$&Angle : $\widehat{CAB}$&Angle : $\widehat{ABC}$\\ Côté adjacent à l'angle : \hbox to1cm{\dotfill}&Côté adjacent à l'angle : \hbox to1cm{\dotfill}&Côté adjacent à l'angle : \hbox to1cm{\dotfill}\\ Côté opposé à l'angle : \hbox to1cm{\dotfill}&Côté opposé à l'angle : \hbox to1cm{\dotfill}&Côté opposé à l'angle : \hbox to1cm{\dotfill}\\ Hypoténuse : \hbox to1cm{\dotfill}&Hypoténuse : \hbox to1cm{\dotfill}&Hypoténuse : \hbox to1cm{\dotfill}\\ $\cos\widehat{ACB}=\dfrac{\strut \ldots\ldots}{\strut \ldots\ldots}$\kern3mm$\sin\widehat{ACB}=\dfrac{\strut \ldots\ldots}{\strut \ldots\ldots}$&$\cos\widehat{CAB}=\dfrac{\strut \ldots\ldots}{\strut \ldots\ldots}$\kern3mm$\sin\widehat{CAB}=\dfrac{\strut \ldots\ldots}{\strut \ldots\ldots}$&$\cos\widehat{ABC}=\dfrac{\strut \ldots\ldots}{\strut \ldots\ldots}$\kern3mm$\sin\widehat{ABC}=\dfrac{\strut \ldots\ldots}{\strut \ldots\ldots}$\\ $\tan\widehat{ACB}=\dfrac{\strut\ldots\ldots}{\strut\ldots\ldots}$&$\tan\widehat{CAB}=\dfrac{\strut\ldots\ldots}{\strut\ldots\ldots}$&$\tan\widehat{ABC}=\dfrac{\strut\ldots\ldots}{\strut\ldots\ldots}$\\ \hline \multicolumn{1}{c|}{\includegraphics{3trigoexo36.4}}&\multicolumn{1}{c|}{\includegraphics{3trigoexo36.5}}&\multicolumn{1}{c}{\includegraphics{3trigoexo36.6}}\\ Angle : $\widehat{ADF}$&Angle : $\widehat{DHC}$&Angle : $\widehat{DBE}$\\ Côté adjacent à l'angle : \hbox to1cm{\dotfill}&Côté adjacent à l'angle : \hbox to1cm{\dotfill}&Côté adjacent à l'angle : \hbox to1cm{\dotfill}\\ Côté opposé à l'angle : \hbox to1cm{\dotfill}&Côté opposé à l'angle : \hbox to1cm{\dotfill}&Côté opposé à l'angle : \hbox to1cm{\dotfill}\\ Hypoténuse : \hbox to1cm{\dotfill}&Hypoténuse : \hbox to1cm{\dotfill}&Hypoténuse : \hbox to1cm{\dotfill}\\ $\cos\widehat{ADF}=\dfrac{\strut \ldots\ldots}{\strut \ldots\ldots}$\hfill$\sin\widehat{ADF}=\dfrac{\strut \ldots\ldots}{\strut \ldots\ldots}$&$\cos\widehat{DHC}=\dfrac{\strut \ldots\ldots}{\strut \ldots\ldots}$\hfill$\sin\widehat{DHC}=\dfrac{\strut \ldots\ldots}{\strut \ldots\ldots}$&$\cos\widehat{DBE}=\dfrac{\strut \ldots\ldots}{\strut \ldots\ldots}$\hfill$\sin\widehat{DBE}=\dfrac{\strut \ldots\ldots}{\strut \ldots\ldots}$\\ $\tan\widehat{ADF}=\dfrac{\strut\ldots\ldots}{\strut\ldots\ldots}$&$\tan\widehat{DHC}=\dfrac{\strut\ldots\ldots}{\strut\ldots\ldots}$&$\tan\widehat{DBE}=\dfrac{\strut\ldots\ldots}{\strut\ldots\ldots}$\\ \hline \multicolumn{1}{c|}{\includegraphics{3trigoexo36.7}}&\multicolumn{1}{c|}{\includegraphics{3trigoexo36.8}}&\multicolumn{1}{c}{\includegraphics{3trigoexo36.9}}\\ Angle : $\widehat{OBA}$&Angle : $\widehat{ASO}$&Angle : $\widehat{SBH}$\\ Côté adjacent à l'angle : \hbox to1cm{\dotfill}&Côté adjacent à l'angle : \hbox to1cm{\dotfill}&Côté adjacent à l'angle : \hbox to1cm{\dotfill}\\ Côté opposé à l'angle : \hbox to1cm{\dotfill}&Côté opposé à l'angle : \hbox to1cm{\dotfill}&Côté opposé à l'angle : \hbox to1cm{\dotfill}\\ Hypoténuse : \hbox to1cm{\dotfill}&Hypoténuse : \hbox to1cm{\dotfill}&Hypoténuse : \hbox to1cm{\dotfill}\\ $\cos\widehat{OBA}=\dfrac{\strut \ldots\ldots}{\strut \ldots\ldots}$\hfill$\sin\widehat{OBA}=\dfrac{\strut \ldots\ldots}{\strut \ldots\ldots}$&$\cos\widehat{ASO}=\dfrac{\strut \ldots\ldots}{\strut \ldots\ldots}$\hfill$\sin\widehat{ASO}=\dfrac{\strut \ldots\ldots}{\strut \ldots\ldots}$&$\cos\widehat{SBH}=\dfrac{\strut \ldots\ldots}{\strut \ldots\ldots}$\hfill$\sin\widehat{SBH}=\dfrac{\strut \ldots\ldots}{\strut \ldots\ldots}$\\ $\tan\widehat{OBA}=\dfrac{\strut\ldots\ldots}{\strut\ldots\ldots}$&$\tan\widehat{ASO}=\dfrac{\strut\ldots\ldots}{\strut\ldots\ldots}$&$\tan\widehat{SBH}=\dfrac{\strut\ldots\ldots}{\strut\ldots\ldots}$\\ \end{tabular} \end{center} }