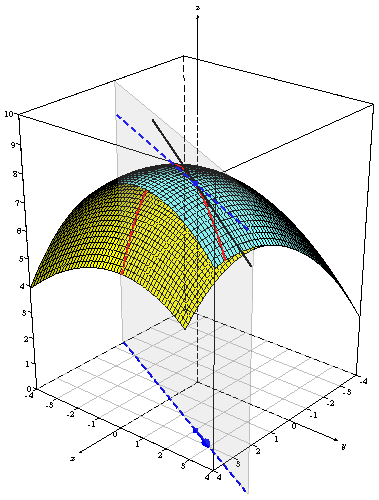
\documentclass{article} % geometric interpretation of directional derivative. %Draft written by Josť Agapito Ruiz \usepackage{pstricks}% \usepackage{pst-solides3d} \usepackage{pst-3dplot}% \thispagestyle{empty} \begin{document} \psset{viewpoint=50 40 30 rtp2xyz,Decran=50}% \psset{lightsrc=viewpoint,linewidth=0.5\pslinewidth}% \begin{pspicture}(-6,-4)(7,12) %\psgrid \psSolid[object=grille,name=baseplane,base=-4 4 -4 4,action=draw,linecolor=lightgray]% \psSurface[% fillcolor=cyan!50, % tracelignedeniveau=true, % hauteurlignedeniveau=5, % linewidthlignedeniveau=3, % couleurlignedeniveau=blue, intersectionplan={[2 -1 0 -3]}, intersectioncolor=(rouge), intersectionlinewidth=1.5, intersectiontype=0, ngrid=.15 .15,incolor=yellow,algebraic, axesboxed,Zmin=0,Zmax=10](-4,-4)(4,4){% (-(x-3)^2-2*(y-1)^2+90)/10 }% %%% lines passing through the points at the domain and at the surface % \psSolid[object=line,args=-0.5 -4 0 4.25 5.5 0,linewidth=1.5pt,linestyle=dashed,linecolor=blue]% line in the direction of (1,2,0) on XY plane \psSolid[object=line,args=-0.5 -4 8.775 4.25 5.5 8.775,linewidth=1.5pt,linestyle=dashed,linecolor=blue]% line parallel to the above one on plane z=8.775 \pstThreeDPut(-1.95,-0.525,7.97){\psSolid[object=line,args=-0.5 -4 0.1 3.5 4 -0.9,linewidth=1.5pt,linecolor=black]}% tangent line to the surface at (2.5,2,8.775) %%% %%% vector % \psSolid[object=vecteur,definition=vecteur3d, args=2 1 0 2.5 2 0,linecolor=blue, linewidth=2pt](2.5,2,0)% vector (1,2,0) %%% %%% points at the surface and at the domain % \psSolid[object=point,args=2.5 2 8.775,dotsize=1pt 1,linecolor=blue]% point at the surface \psSolid[object=point,args=2.5 2 0,dotsize=1pt 1,linecolor=blue]% point at the domain %%% %%% transparent plane perpendicular to XY plane and in the direction of vector %(1,2,0) % \psSolid[fillcolor=white!40,opacity=0.2,object=plan, definition=equation,args={[2 -1 0 -3]}, base=-5.3 7.4 -4 7.5](-3.6,-4.5,0)% %%% \end{pspicture} \end{document}