droite_01.tex

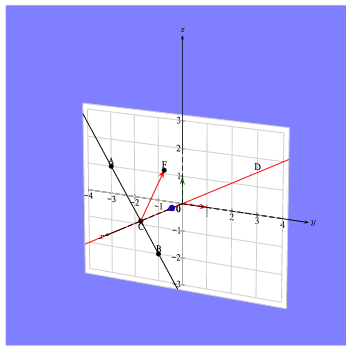
\documentclass{article}
\usepackage{pst-solides3d}
\begin{document}
\pagestyle{empty}
 
\begin{pspicture}(-6,-5)(6,8)%
\psframe*[linecolor=blue!50](-6,-5)(6,7)
\psset{lightsrc=viewpoint,viewpoint=50 30 15,Decran=60}
\psset{solidmemory}
\defFunction[algebraic]{F1}(x){3*sin(x)}{}{}
%% definition des plans
%% exemple 1
\psSolid[object=plan,
   definition=equation,
   args={[1 0 0 0] 90},
   base=-4.2 4.2 -3.2 3.2,
   name=monplan,
   fillcolor=white,
   linecolor=gray!40,
   plangrid,
   planmarks,
   showBase,
]
\psset{plan=monplan}
%% construction et nommage d'une droite D
%% passant par (0,0) et (2,1)
\psProjection[object=droite,
   args=0 0 2 1,
   name=D1,
   linecolor=red,
]
%% label de la droite, au point d'abscisse 3
\psProjection[object=point,
   definition=xdpoint,
   args=3 D1,
   text=D,
   pos=uc,
   action=none,
]
%% definition du point A
\psProjection[object=point,
   args=-3 1,
   name=A,
   text=A,
   pos=uc,
]
%% definition du point B
\psProjection[object=point,
   args=-1 -2,
   name=B,
   text=B,
   pos=uc,
]
%% droite (AB) = D2
\psProjection[object=droite,
   args=A B,
   name=D2,
]
%% intersection des droites D1 et D2
\psProjection[object=point,
   definition=interdroites,
   args=D1 D2,
   name=C,
   text=C,
   pos=dc,
]
%% definition du vecteur U
\psProjection[object=vecteur,
   args=1 2,
   linecolor=red,
   name=U,
](C,)
%% point F tel que vect(CF) = U
\psProjection[object=point,
   definition=translatepoint,
   args=C U,
   text=F,
   pos=uc,
]
\composeSolid
\axesIIID(4,4,2)(5,5,6)
\end{pspicture}
 
 
\end{document}