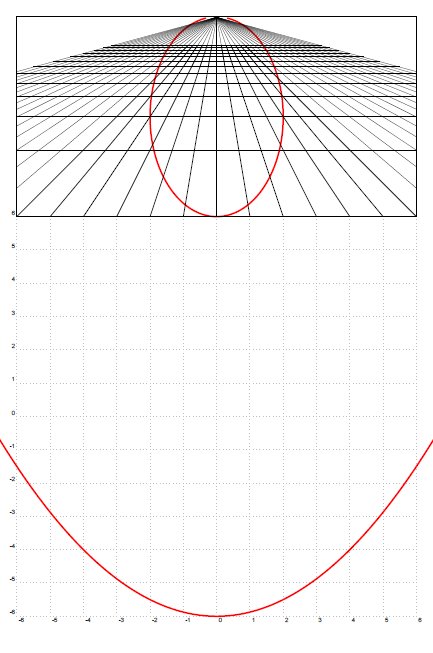
\documentclass[12pt]{article} \usepackage{pst-anamorphosis-add,pst-plot,pst-grad} \usepackage[T1]{fontenc} \usepackage[ansinew]{inputenc} \usepackage[frenchb]{babel} \usepackage{amsmath,amssymb} \usepackage[a4paper]{geometry} \usepackage{url} \makeatletter \def\psparametricplotA{\pst@object{parametricplotA}}% hv 2008-11-22 \def\parametricplotA{\pst@object{parametricplotA}} \def\parametricplotA@i#1#2{\@ifnextchar[{\parametricplotA@x{#1}{#2}}{\parametricplotA@x{#1}{#2}[]}} \def\parametricplotA@x#1#2[#3]{\@ifnextchar[{\parametricplotA@xi{#1}{#2}[#3]}{\parametricplotA@xi{#1}{#2}[#3][]}} \def\parametricplotA@xi#1#2[#3][#4]#5{% \pst@killglue% \begingroup% \use@par% \@nameuse{beginplot@\psplotstyle}% \addto@pscode{% \tx@optionsanamorphosis \tx@optionsanamorphosisAdd #3 %prefix PS code \psplot@init /t #1 def /t1 #2 def /dt t1 t sub \psk@plotpoints div def /F@pstplot \ifPst@algebraic (#5) \ifx\psk@PlotDerivative\@none\else \psk@PlotDerivative\space { (t) tx@Derive begin Derive end } repeat \fi\space tx@AlgToPs begin AlgToPs end cvx \else { #5 } \fi def \ifPst@VarStep /StillZero 0 def /LastNonZeroStep dt def /F2@pstplot tx@Derive begin (#5) (t) Derive (t) Derive end \ifx\psk@PlotDerivative\@none\else \psk@PlotDerivative\space { (t) tx@Derive begin Derive end } repeat \fi\space tx@AlgToPs begin AlgToPs end cvx def %% computation of the tolerance defined by plotpoints /epsilon12 \ifx\psk@VarStepEpsilon\@default tx@Derive begin F2@pstplot end Pyth dt 3 exp abs mul \else\psk@VarStepEpsilon\space 12 mul \fi def /ComputeStep { dup 1e-4 lt { pop StillZero 2 ge { LastNonZeroStep 2 mul } { LastNonZeroStep } ifelse /StillZero StillZero 1 add def } { epsilon12 exch div 1 3 div exp /StillZero 0 def } ifelse } bind def \fi /xy { \ifPst@algebraic F@pstplot \else #5 \fi \pst@number\psyunit mul exch \pst@number\psxunit mul exch tx@anamorphosisPathDict begin Anamorphose end } def }% \gdef\psplot@init{}% \@pstfalse \@nameuse{testqp@\psplotstyle}% \if@pst\parametricplotA@ii{#4}\else\parametricplotA@iii{#4}\fi \endgroup% \ignorespaces} % \def\parametricplotA@ii#1{% para is the post code \ifPst@VarStep% \addto@pscode{% mark xy \@nameuse{beginqp@\psplotstyle} { F2@pstplot Pyth ComputeStep t 2 copy add dup t1 gt {pop t1} if /t exch def F2@pstplot Pyth ComputeStep /t 3 -1 roll def 2 copy gt { exch } if pop /t t 3 -1 roll add dup t1 gt {pop t1} if def xy \@nameuse{doqp@\psplotstyle} t t1 eq { exit } if } loop}% \else\pst@killglue% \addto@pscode{% /ps@Exit false def xy \@nameuse{beginqp@\psplotstyle} \psk@plotpoints 1 sub { /t t dt add def xy \@nameuse{doqp@\psplotstyle} ps@Exit { exit } if } repeat ps@Exit not { /t t1 def xy \@nameuse{doqp@\psplotstyle} } if }% \fi% \addto@pscode{ #1 }% \@nameuse{endqp@\psplotstyle}} % \def\parametricplotA@iii#1{% \ifPst@VarStep% \addto@pscode{% /n 2 def mark { xy n 2 roll F2@pstplot Pyth ComputeStep t 2 copy add dup t1 gt {pop t1} if /t exch def F2@pstplot Pyth ComputeStep /t 3 -1 roll def 2 copy gt { exch } if pop /t t 3 -1 roll dup /LastNonZeroStep exch def add dup t1 gt {pop t1} if def /n n 2 add def t t1 eq { exit } if } loop xy n 2 roll}% \else\pst@killglue% \addto@pscode{ mark /n 2 def \psk@plotpoints { xy n 2 roll /n n 2 add def /t t dt add def } repeat /t t1 def xy n 2 roll}% \fi% \addto@pscode{ #1 }% \@nameuse{endplot@\psplotstyle}} % \makeatother \title{pst-anamorphosis : la comète de Halley} \author{ML} \date{4 novembre 2011} \begin{document} \maketitle % Cet exemple est inspiré par la lecture de l'article de la revue Tangente \No{}1 : \textit{La courbe du mois : La parabole}, où l'auteur J.Lubczanski traite du cas particulier de la trajectoire parabolique d'un corps et donne en exemple la comète de Halley : \og elle vient de si loin que sa trajectoire est parabolique au voisinage de la Terre \fg. L'auteur donne ensuite un dessin en perspective (de J.Lefort) dans lequel on voit que lorsque la trajectoire de la comète est vue en perspective \og la parabole se ``\textit{referme}'' à l'infini\fg et peut ainsi être confondue avec une ellipse. \textcolor{blue}{\url{http://www.uwgb.edu/dutchs/PLANETS/Comets.HTM}} Cet exemple peut très bien s'illustrer avec le package \textsf{pst-anamorphosis} et l'option \textsf{[type=perspective]}. On utilise pour cela la commande \verb+\parametricplotA+ : \begin{verbatim} \parametricplotA[plotpoints=1000,linecolor=red,linewidth=0.5mm]{-50}{50}{% t t dup mul 8 div 6 sub } \end{verbatim} On pourra éventuellement consulter l'exercice de physique ayant pour thème la comète de Halley et donné dans l'épreuve de physique à la session 1999 du baccalauréat. \textcolor{blue}{\url{http://manuel.luque.perso.neuf.fr/Halley/}} \begin{center} \begin{pspicture}(-6,-6)(6,12) \psgrid[subgriddiv=0,gridcolor=lightgray,griddots=10,gridlabels=5pt](-6,-6)(6,6) \psset{type=perspective} \psset{ua=6,F=12,D=2} \pstVerb{/sqrt_2 0.707 def}% \parametricplot[plotpoints=1000,linecolor=red,linewidth=0.5mm]{-10}{10}{% t t dup mul 8 div 6 sub } \parametricplotA[plotpoints=1000,linecolor=red,linewidth=0.5mm]{-50}{50}{% t t dup mul 8 div 6 sub } \psset{linewidth=0.5\pslinewidth} \multido{\i=-6+1}{13}{% \pnode(! \i\space -6){A} \pnode(! \i\space 6){B} % \psline(A)(B) \pslineA(A)(B) }% \multido{\i=-6+1}{13}{% \pnode(!-6 \i){A} \pnode(!6 \i){B} \pslineA(A)(B) % \psline(A)(B) }% \psclip{\psframe(-6,6)(6,12)} \multido{\i=-6+1}{13}{ \pnode(!0 1000){A} \pslineA(\i,0)(A)} \multido{\i=-22+1}{16}{ \pnode(!0 1000){A} \pslineA(\i,-6)(A)} \multido{\i=22+-1}{16}{ \pnode(!0 1000){A} \pslineA(\i,-6)(A)} \multido{\i=-6+1}{13}{ \pslineA(-22,\i)(22,\i)} \endpsclip \end{pspicture} \end{center} \end{document}