


2.6 La caméra
Les étudiants en arts s'entraînent parfois à la perspective en dessinant sur une fenêtre avec un crayon gras, c'est une transformation mathématique appelée projection conique. L'application qu'ePiX utilise par défaut pour projeter le monde sur l'écran lui ressemble. Imaginez-vous au point de vue et doté d'un regard aux rayons X qui rend pour vous tous les objets transparents. Quelque part devant vous se trouve l'écran, un plan. La cible est le le point de l'écran pied de la perpendiculaire au plan passant par le point de vue.
Trois vecteurs unité mutuellement perpendiculaires ont leur origine à la cible : mer, ciel et ½il. Le vecteur mer pointe vers la droite, le ciel pointe vers le haut et l'½il suit la direction qui relie la cible au point de vue. La boite-cadre de la figure est définie dans le repère (cartésien) mer-ciel de l'écran.
Soit un point p devant le point de vue, nous voulons détermine l'endroit de l'écran où il se projette. Traçons une droite joignant p et le point de vue, cette droite perse le plan de l'écran une fois et une seule, c'est en ce point d'intersection que nous traçons p sur l'écran.
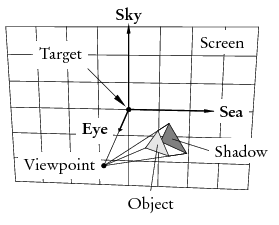
Figure 2.3: Projection d'un point.
Au début de la figure, la caméra3 est placée sur l'axe z à une très grande distance de l'origine. La vue qui en résulte, essentiellement une projection parallèle à l'axe z convient aux figures planes. On manipule la caméra avec une syntaxe orientée objet :
camera.at(P posn); // fixe le point de vue à posn
camera.look_at(P targ); // fixe la cible
camera.range(double dist);
// fixe la cible, déplace le point de vue
camera.focus(double dist);
// fixe le point de vue, déplace la cible
camera.rotate_sea(double angle); // rotation autour d'un axe
Ces commandes doivent être placées dans le corps de la figure.
- 3
- Note du TdS : Le mot anglais camera signifie « appareil photographique» mais j'ai préféré « caméra» qui a pour seul avantage celui de la brièveté.


