3.7 Graphes et domaines
On utilisera le mot « application» (map) pour désigner une fonction C++ d'un ou plusieurs arguments double retournant un double ou un P. Mathématiquement, une application peut être représentée de deux façons : avec un graphe (qui retient l'information quant au domaine) ou avec une courbe paramétrée (qui se débarasse du domaine). ePiX fait l'hypothèse qu'une application à valeur double doit être représentée par un graphe et qu'une application à valeur P doit l'être par une courbe paramétrée. Dans les deux cas on parlera de « graphique» (plot). Les graphiques d'ePiX sont soit « en mailles» (wire mesh), obtenus avec une commande plot, soit « ombrée» (shaded), obtenus par la commande surface.
Un domain (domaine) d'ePiX comprend une boite de coordonnées, définie par une paire de coins opposés, et deux maillages (meshes) qui précisent la quantité de données à représenter. Pour des graphiques sélectifs un domain peut être découpé et retaillé. On décrit ces opérations en détail plus loin.
Les arguments d'une commande plot sont une application suivie soit d'un domaine soit de quelque chose logiquement équivalent. Par exemple :
double f(double t) { return t*t; }
P F(double u, double v) { return P(u, v, exp(u)*Sin(v)); }
P G(double u, double v, double w) { return P(v*w, u*w, u*v); }
// [0,3] x [-1,2]: 12 x 6 rectangles, 60 x 60 intervalles
domain R(P(0,-1), P(3,2), mesh(12,6), mesh(60,60));
// [-1,1] x [-1,1] x [0,1] divisé de manière analogue
domain R3d(P(-1,-1,0), P(1,1,1), mesh(4,8,5), mesh(60,48,120));
plot(f, -2, 2, 60);// f:[-2,2] -> R, en utilisant 60 intervalles
plot(F, R); // graphe de exp(u)*Sin(v)
plot(G, R3d.slice2(0.5); // G: R^3 -> R^3 restreinte à y=0.5
Par convention (que le compilateur fait respecter) des commandes plot utilisant des applications à valeur P acceptent un argument domain comme dans les deuxième et troisième commandes ci-dessus. Pour représenter une fonction à valeur double, en revanche, il faut fournir un équivalent logique d'un domain, habituellement les extrémités et le nombre d'intervalles, comme dans la première commande plot ci-dessus.
Supposons que le domain R2 est, comme ci-dessus, le rectangle [0,3]×[−1,2]. L'argument mesh(12,6) le divise en un réseau de 12×6 sous-rectangles connu sous le nom de maillage grossier (coarse mesh). Une application de deux variables à valeur P est représentée au-dessus du réseau du maillage grossier. Toutefois, plutot que de tracer des quadrilatères, ePiX trace les courbes images à la résolution définie par l'argument mesh(60,60), le maillage fin (fine mesh). Dans cet exemple, les courbes sont dessinées, dans chaque direction, en utilisant 60 segments de droite.
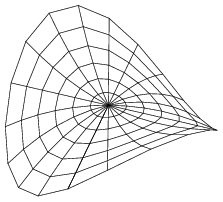
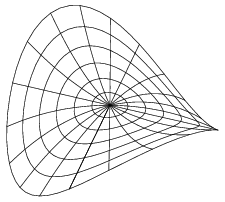
La séparation des roles des maillages grossier et fin permet à un graphe en mailles de suivre de près une surface sans utiliser une grille fine de courbes. Les deux parties de la figure 3.2 sont tracées avec un maillage grossier de 6×20. Dans la première figure, le maillage fin est aussi 6×20 alors que dans la seconde il est 12×60.
Le maillage grossier n'a de sens que pour des domaines de dimension supérieure ou égale à 2. La taille du maillage grossier détermine le nombre de courbes ou de surfaces tracées perpendiculairement à la direction d'une coordonnée tandis que le maillage fin détermine le nombre de segments utilisés le long de cette direction. Pour obtenir des résultats prévisibles le maillage fin devrait être un petit multiple du maillage grossier.
Les graphiques se comportent de manière analogue pour des domains en dimension 3 et des applications de trois variables : le « squelette de dimension 1» de l'image du domain est tracé. De plus, une application de trois variables à valeur P peut être tracée au-dessus d'un domain de dimension 1 ou 2. Toutefois, l'effet peut être inattendu à moins que le domaine n'ait été obtenu par découpage (slicing). On ne peut pas tracer une application d'une ou deux variables au-dessus d'un domain de dimension 3.
Opérateurs sur les domaines
Un domaine peut être retaillé suivant chaque axe de coordonnées pour lequel l'épaisseur est positive :
domain R(P(0,0), P(2,1), mesh(12,12), mesh(36,36)); // [0,2] x [0.5,0.75], grossier 12 x 3, fin 36 x 9 domain R_new = R.resize2(0.5,0.75);
Retailler permet de représenter une application restreinte à un ensemble de parties de son domaine. On peut s'en servir pour insister sur des parties de l'image, couper en couches des éléments de la scène, rapiécer des surfaces etc.
Autant que possible, la retaille conserve les tailles absolues des quadrillages. Pourtant, en général, on tronque. Pour le domaine ci-dessus, R.resize2(0,0.2) aurait un maillage grossier de 12× 2 (car 12/5=2,4→ 2) et un fin de 36× 7. Pour éviter un comportement inattendu, choisissez des tailles de maillage telle qu'une retaille n'entaine pas de troncature des entiers.
Un domaine peut être tranché en rendant constante une des variables. Le résultat est un domaine dont le nombre de dimension est inférieur d'une unité de celui originel. Avec le R de ci-dessus, R.slice1(0.3) est le domain de dimension 1 {0,3×[0,1]} avec un maillage grossier de 1 × 12 et un fin de 1× 36.
Quand on représente une famille d'application, un domain a des opérateurs slices (tranches) qui retourne la liste des domains obtenus en tranchant suivant une variable selon des constantes régulièrement espacées. Un argument optionnel fixe le nombre de tranches. Il n'est pas nécessaire que cet argument soit relié au maillage grossier.
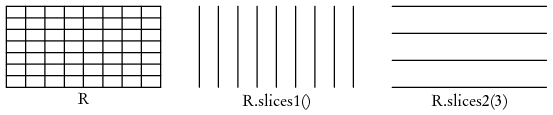
On peut utiliser les commandes de taille et de tranchage directement dans une
commande plot :
plot(F, R.resize(0,0.5)); plot(F, R.slices1());
Surfaces ombrées
ePiX fournit les outils pour représenter des surfaces ombrées, cf. également la section 4.1. Si le remplissage est activé, une surface est ombrée suivant l'angle du vecteur normal avec la direction de la caméra, donnant l'effet d'un éclairage ambient constant. Autrement, on utilise le gris courant – 0,3 par défaut.
La commande surface à la même syntaxe que la commande plot lorsqu'on ne trace qu'une seule surface. En général, le retrait des objets cachés demande quelques différences. Une commande ePiX écrit une strophe dans un fichier de sortie ; les éléments de la scène sont dessinés dans leur ordre dans le fichier d'entrée. Une scène contenant une ou plusieurs surfaces opaque ne peut pas être construire surface par surface. Au contraire, les différentes surfaces doivent être assemblées dans une unique structure de données avant qu'on puisse les dessiner.
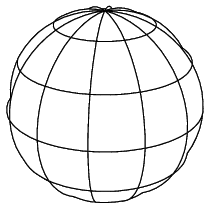
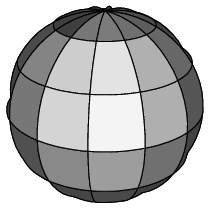
Comme dans la représentation en mailles, le maillage fin est utilisé pour tracer les frontières des pièces de surface, cela tend à représenter les surfaces plus souplement pour de faibles tailles du maillage grossier. Si le maillage grossier l'est trop, toutefois, deux effets visuels indésirables peuvent apparaitre. Premièrement, des régions adjacentes de la surface peuvent être ombrées très différemment puisque l'ombrage est constant sur chaque pièce définie par le maillage grossier (voir la 2image à partir de la gauche de la figure 3.3). Deuxièmement, une pièce presque tangente à une ligne de visée peut être mal tracée si la pièce se replie vers l'arrière puisque l'on trace la frontière de la pièce et pas les bords visibles de la surface mathématique (voir la figure 3.3, les deux images de gauche.)

Figure 3.3: Effets de maillage grossier – tous les maillages fins sont identiques.
Surface unique
La commande surface(F, R) représente la fonction F à valeur P sur le domaine R, elle est l'équivalent « ombré» de la commande plot correspondante. ePiX fournit aussi des commandes spéciales pour les surfaces de révolution :
void surface_rev(f, t_min, t_max, n_lats, n_longs); void surface_rev(f, g, t_min, t_max, n_lats, n_longs);
La première fait tourner le graphe de f autour de l'axe des x, la
seconde utilise la courbe paramétrée t↦(f(t),g(t)) comme
profil. Dans chaque cas, le paramètre intervalle [t_min,t_max] est divisé
en n_lats sous-intervalles de même amplitude, n_longs copies du
profil (24 par défaut) sont tracés et la surface complète (une révolution
complète) est tracée.
Une troisième forme de la commande utilise un argument domain pour controler l'étendue des longitudes et dessine la surface de révolution dans un repère cartésien défini par la base orthonormale coords – par défaut, la base canonique. Les arguments f et g définissent une courbe paramétrique dans le plan des deux premiers éléments de coords et le premier élément définit l'axe de rotation.
void surface_rev(f, g, R, frame coords);
Surfaces multiples
L'algorithme de traitement des surfaces cachées d'ePiX-1.x découpait la surface en pièces suivant le maillage, les triaient dans l'ordre (approximativement) décroissant de distance à la caméra et les imprimait. Cette technique fonctionnait assez correctement pour des surfaces sans intersection et restait même acceptable pour manipuler des surfaces sécantes dont les mailles se coupaient suivant leurs frontières.
Les surfaces multiples sont construites à partir d'une ou plusieurs applications et d'un ou plusieurs domains de dimension 2. Dans l'extrait de code ci-dessous, F et G sont des fonctions de 3 variables à valeur P et R est un domain de dimension 3.
Pour représenter les images de plusieurs domains par une seule application, il faut grouper les domains dans une liste puis émettre la commande surface :
surface(F, R.slices3()); domain_list DL(R.slice1(0)); // construit la liste de domaines DL.add(R.slice2(0.5)); // ajoute un domaine DL.add(R.slices3()); // etc. surface(G, DL); // dessine
Pour traiter des applications multiples, ePiX fournit une classe scenery (paysage). Conceptuellement, une scenery est une agglomération de surfaces ombrées, construite l'une après l'autre à partir d'applications et de domains de dimension 2. La fonction add accepte deux arguments – une application et soit un domain soit une liste de domains – et offre ses données à la scenery au lieu de les tracer immédiatement. La scenery complète est tracée par un appel fait à la main :
scenery S(F, R.slice3(0.25)); // S contient une surface S.add(F, R.slice2(0)); // S contient deux surfaces S.add(G, R.slices1(2)); // S contient cinq surfaces S.draw();
Consultez les fichiers d'exemples spherical.xp et minkowski.xp dans le répertoire extras pour des exemples complets.
En principe, une scène peut contenir un nombre arbitraire de surfaces et l'écriture du fichier eepic ne pose aucun problème. Toutefois une figure qui contient beaucoup d'objets tend à peser sur les piles internes de LATEX. De fréquents changements de couleur exarbent le problème. À moins d'accroitre la mémoire de LATEX, il est peu vraissemblable qu'une figure contenant plus d'un millier d'éléments maillés compile, même dans une résolution modeste, une surface peut facilement contenir 1000 pièces de gris d'intensités diverses. Mais cela peut dépendre de votre installation.
Fonctions utilitaires
Dans cette section, f et g sont deux fonctions d'une variable à valeur double. ePiX définit des fonctions numériques qui retourne le maximum ou le minimum sur un intervalle, une approximation des racines et qui travaillent avec les dérivées et les intégrales définies.
sup(f, a, b); // max/min de f sur [a,b] inf(f, a, b); newton(f, g, x0); // trouve une approximation du point d'intersection
La méthode de Newton retourne le point d'intersection de deux fonctions données, en partant de la graine donnée qui devrait être raisonnablement proche de la solution attendue. Si on tombe sur un point critique ou si on accomplit cinq itérations sans amélioration un avertissement apparait et le résultat courant (probablement incorrect) est retourné6. La seconde fonction g est la constante nulle si elle n'est pas spécifiée.
On utilise les classes Deriv et Integral pour le calcul des dérivées et intégrales numériques et pour représenter graphiquement ces fonctions.
Deriv df(f); // objet fonction : df(x) = f'(x) df.eval(t); // retourne f'(t) df.left(t); // derivée à gauche en t: (f(t)-f(t-dt))/dt df.right(t); // derivée à droite en t: (f(t+dt)-f(t))/dt Integral prim(f,a); // objet fonction: prim(x) = int_a^x f prim.eval(b); // intégrale numérique de f sur [a,b] double val(Integral(f).eval(1)); // val = \int_0^1 f
La limite inférieur de l'intégrale vaut 0 par défaut.
Les tangentes et les enveloppes (familles de tangentes) sont dessinées avec
tan_line(f, t); // f real- or vector-valued envelope(f, t_min, t_max, n); // family of tangent lines tan_field(f1, f2, t_min, t_max, n); // field of tangents
Les fichiers d'exemples conic.xp et lissajous.xp illustrent ces capacités.
Graphiques et analyse
ePiX peut représenter la dérivée ou une primitive des fonctions réelles et représenter les sommes de Riemann pour les intégrales définies. Soit f une fonction réelle d'une seule variable.
plot(Deriv(f), a, b, n); // graphe de f' sur [a,b] plot(Integral(f, x0), a, b, n); riemann_sum(f, a, b, n, TYPE);
La deuxième commande trace la primitive définie par x↦∫x0x f(t) dt sur [a,b] où, comme avant, x0 vaut 0 par défaut. La troisième trace les rectangles ou les trapèzes dont la somme des aires approche l'intégrale définie de f sur [a,b]. Le TYPE peut être UPPER, LOWER, LEFT, RIGHT, MIDPT ou TRAP.
ePiX résoud les équations les équations différentielles ordinaires (abr. anglaise ODE) en deux ou trois variables et représente les champs de vecteurs (champ des vitesses) et de tangentes (slope field) et de tangentes orientées (dart field). Soit F une fonction de deux ou trois variables à valeur P.
ode_plot(F, p_0, t_min, t_max, n); flow(F, p_0, t_max, n);
La première commande représente la solution du problème avec condition initiale ẋ=F(x), x(0)=p0 sur l'intervalle de temps précisé. Si tmin est omis, sa valeur est 0 et la courbe démarre à p0. Avec quelques manipulations pour faire pivoter un champ plan d'un quart de tour, on peut utiliser ode_plot pour tracer les courbes de niveau d'une fonction de deux variables, cf. le fichier d'exemple dipole.xp. La fonction flow retourne la valeur (approchée) obtenue en partant de p0 et en appliquant la méthode d'Euler à n pas de résolution de l'équation ẋ=F(x)., ce qui est utile pour placer avec précision des marques ou des têtes de flèches le long d'une courbe intégrale.
On peut obtenir la représentation d'un champ de vecteurs (dans un plan ou l'espace) au-dessus d'un domaine R de trois façons :
vector_field(F, R, [scale]); // vraie longueur dart_field (F, R, [scale]); // longueur constante slope_field (F, R, [scale]); // longueur constante
On échantillone le champ aux n½uds du maillage grossier. Si le domaine est de dimension 2, le graphe est une tranche plane du champ, même si le champ dépend de trois variables. Si le domaine est de dimension 3, le champ est dessiné dans des tranches successives z =const en partant de la hauteur du premier coin de R et finir à la hauteur du second.
Le dernier argument facultatif, qui vaut 1 par défaut, est un facteur d'homothétie des têtes de flèches d'un champ de vecteurs et de la longueur (constante) des vecteurs dans les champs obtenus par dart_field ou slope_field. Le fichier d'exemple extras/vfield.xp illustre ces capacités, y compris l'utilisation des styles de lignes de PSTricks pour réaliser l'effacement des objets cachés.
Dans chaque commande de représentation de champ, l'argument de type domaine peut être remplacé par deux points – représentant les coins d'un rectangle de coordonnées – et deux entiers – le nombre d'intervalles de quadrillage dans les directions de coordonnées choisies. On ne peut représenter que des tranches planes de champ de vecteurs dans cette syntaxe de rechange.
Courbes fractales récursives
Considérons un chemin fait de segments de même longueur qui peuvent être orienté
par n'importe quel angle de la forme 2π k/n radians pour 0⩽
k<n, comme les dents d'un engrenage. Un chemin est donné par une suite finie
d'entiers, pris modulo n. Par exemple, si n=6 alors la suite 0, 1, −1,
0 correspond au chemin ASCII _/\_. Une approximation d'une fractale par
ePiX commence avec une telle « graine» (seed) puis remplace
récursivement – jusqu'à une profondeur (depth) donnée – chaque segment
avec une copie réduite et pivotée de la graine. La graine ci-dessus engendre la
fractale connue comme « flocon de von Koch». En voici le code :
const int seed[] = {6, 4, 0, 1, -1, 0};
fractal(P(a,b), P(c,d), depth, seed);
La première donnée de seed[] (6 ici) est le nombre n de « dents», le second (4) est le nombre de termes de la graine et le reste constitue la graine proprement dite. Le chemin final joint (a,b) à (c,d). Le nombre de segments dans le chemin final croît de façon exponentielle avec la profondeur, aussi des profondeurs supérieures à 5 ou 6 risque vraisemblablement de dépasser les capacités de LATEX ou PostScript.

Figure 3.4: Itérations successives de {4,8,0,1,0,3,3,0,1,0}
- 6
- Note du TdS : À ma demande, l'auteur précise ce qui suit : Pour ePiX « convergence»signifie obtenir une racine avec une précision d'environ 10−5 donc si cinq itérations n'ont pas suffit, l'utilisateur devrait pouvoir faire mieux.