Pavages triangulaires
%%D'apres 'Pour la science' n°272 Avril 2000 - p106
input geometriesyr12;
vardef pavagesequi(expr chemin,tour,coul,coull)=
save $;
picture $;
pair A,B,C;
A=u*(0,0);
B=u*(1,0);
C=rotation(B,A,60);
path especes;
especes = chemin
-- rotation(chemin,symetrie(iso(A,B,C),A,B),-120)
-- rotation(chemin,symetrie(iso(A,B,C),A,B),120)
-- cycle;
if tour=0:
$=image(
trace chemin;
);
elseif tour=1:
$=image(
fill especes withcolor coul;
fill (chemin--symetrie(chemin,iso(A,B))--cycle) withcolor coull;
trace especes;
trace symetrie(chemin,iso(A,B));
A:=symetrie(C,A);
B:=symetrie(C,B);
);
elseif tour>=2:
$=pavagesequi(chemin,1,coul,coull);
for k=2 upto tour:
$:=image(
trace $;
trace rotation($,symetrie(iso(A,B,C),A,B),-120);
trace rotation($,symetrie(iso(A,B,C),A,B),120);
trace symetrie($,iso(A,B));
A:=symetrie(C,A);
B:=symetrie(C,B)
);
endfor;
fi;
$
enddef;
vardef pavagesequiqui(expr chemin,tour,coul,coull)=
save $;
picture $;
pair A,B,C;
A=u*(0,0);
B=u*(1,0);
C=rotation(B,A,60);
path especes;
especes = chemin
-- rotation(chemin,symetrie(iso(A,B,C),A,B),-120)
-- rotation(chemin,symetrie(iso(A,B,C),A,B),120)
-- cycle;
if tour=0:
$=image(
trace chemin;
);
elseif tour=1:
$=image(
trace chemin;
drawoptions(dashed evenly);
trace rotation(chemin,symetrie(iso(A,B,C),A,B),-120);
trace rotation(chemin,symetrie(iso(A,B,C),A,B),120);
trace symetrie(chemin,iso(A,B));
drawoptions();
A:=symetrie(C,A);
B:=symetrie(C,B);
);
elseif tour=2:
$=image(
fill especes withcolor coul;
fill (chemin--symetrie(chemin,iso(A,B))--cycle) withcolor coull;
trace especes;
trace symetrie(chemin,iso(A,B));
A:=symetrie(C,A);
B:=symetrie(C,B);
);
$:=image(
trace $;
drawoptions(dashed evenly);
trace rotation(pavagesequi(chemin,1,coul+0.5blanc,coull+0.5blanc),
symetrie(iso(A,B,C),A,B),-120);
trace rotation(pavagesequi(chemin,1,coul+0.5blanc,coull+0.5blanc),
symetrie(iso(A,B,C),A,B),120);
trace symetrie(pavagesequi(chemin,1,coul+0.5blanc,coull+0.5blanc),
iso(A,B));
drawoptions();
A:=symetrie(C,A);
B:=symetrie(C,B);
);
elseif tour>=3:
$=pavagesequi(chemin,1,coul,coull);
for k=2 upto tour-1:
$:=image(
trace $;
trace rotation($,symetrie(iso(A,B,C),A,B),-120);
trace rotation($,symetrie(iso(A,B,C),A,B),120);
trace symetrie($,iso(A,B));
A:=symetrie(C,A);
B:=symetrie(C,B);
);
endfor;
$:=image(
trace $;
drawoptions(dashed evenly);
trace rotation(pavagesequi(chemin,tour-1,coul+0.5blanc,coull+0.5blanc),
symetrie(iso(A,B,C),A,B),-120);
trace rotation(pavagesequi(chemin,tour-1,coul+0.5blanc,coull+0.5blanc),
symetrie(iso(A,B,C),A,B),120);
trace symetrie(pavagesequi(chemin,tour-1,coul+0.5blanc,coull+0.5blanc),
iso(A,B));
drawoptions();
A:=symetrie(C,A);
B:=symetrie(C,B);
);
fi;
$:=image(
trace $;
trace A--B--C--cycle
dashed dashpattern(on12bp off6bp on3bp off6bp) withcolor gris;
trace iso(A,B)--iso(B,C)--iso(C,A)--cycle
dashed dashpattern(on12bp off6bp on3bp off6bp) withcolor gris;
);
$
enddef;
 beginfig(1);
path MM;
MM=(0,0)--u*(0.25,0)--u*(0.25,0.4)--u*(0.75,0.2)--u*(1,0);
trace pavagesequiqui(MM,0,orange,vert);
endfig;
beginfig(1);
path MM;
MM=(0,0)--u*(0.25,0)--u*(0.25,0.4)--u*(0.75,0.2)--u*(1,0);
trace pavagesequiqui(MM,0,orange,vert);
endfig;
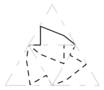 beginfig(2);
trace pavagesequiqui(MM,1,orange,vert);
endfig;
beginfig(2);
trace pavagesequiqui(MM,1,orange,vert);
endfig;
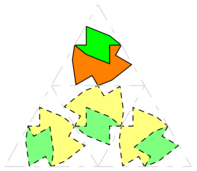 beginfig(3);
trace pavagesequiqui(MM,2,orange,vert);
endfig;
beginfig(3);
trace pavagesequiqui(MM,2,orange,vert);
endfig;
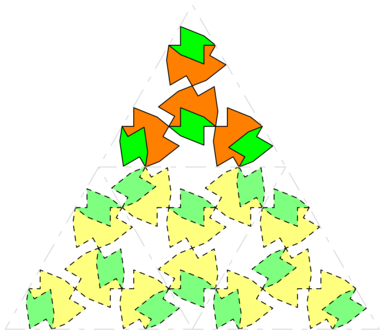 beginfig(4);
trace pavagesequiqui(MM,3,orange,vert);
endfig;
beginfig(4);
trace pavagesequiqui(MM,3,orange,vert);
endfig;
 beginfig(5);
trace pavagesequiqui(MM,4,orange,vert);
endfig;
end
beginfig(5);
trace pavagesequiqui(MM,4,orange,vert);
endfig;
end
beginfig(1); path MM; MM=(0,0)--u*(0.25,0)--u*(0.25,0.4)--u*(0.75,0.2)--u*(1,0); trace pavagesequiqui(MM,0,orange,vert); endfig;
beginfig(2); trace pavagesequiqui(MM,1,orange,vert); endfig;
beginfig(3); trace pavagesequiqui(MM,2,orange,vert); endfig;
beginfig(4); trace pavagesequiqui(MM,3,orange,vert); endfig;
beginfig(5); trace pavagesequiqui(MM,4,orange,vert); endfig; end