Compléments théoriques
pour PST-MIRROR

Manuel LUQUE

11 août 2002
Résumé
Pour illustrer ces compléments, j’utilise le package PST-R3D qui est une adaptation, que j’ai faite, de PST-3D à la perspective cavalière. Dans ce package Timothy Van Zandt avait eu l’idée très ingénieuse de construire la matrice de transformation courante : CTM de PostScript à partir des formules de transformation permettant de représenter en projection parallèle dans une direction donnée par les coordonnées de [viewpoint = pxpypz] un plan défini par une normale à ce plan [normal = nxnynz] et un point origine appartenant à ce plan.

J’ai repris cette idée dans PST-R3D, et bien sûr dans ce qui nous intéresse : la vison d’un objet dans une boule-miroir, c’est-à-dire dans le package PST-MIRROR, pour le cas particulier de la définition d’un plan.

Formules de transformation

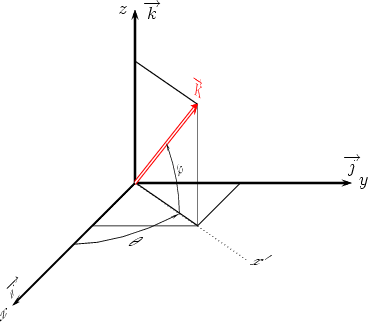
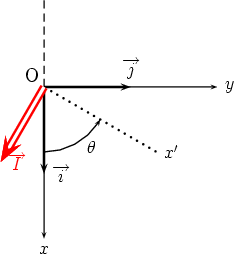
Formules permettant de passer du repère (O, 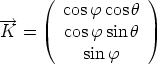--->I, --->J, --->K) au repère (O, ---> i, ---> j, ---> k)
---> K représentera la normale au plan que l’on souhaite dessiner en perspective cavalière. Ce vecteur ---> K est défini par la longitude h et la latitude f.

Dans (O, ---> i, ---> j, ---> k)

( ) ---> cos f cosh K = cos f sin h sin f
Il faut ensuite choisir les deux autres vecteurs de la base (--->I, --->J, --->K). Je choisis de garder ---> I dans le plan Oxy.
--->--->---> ---> kzjyxhKfx' i
Vu de dessus, dans le plan Oxy :

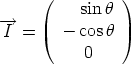( ) ---> sinh I = - cosh 0
yxO--->i--->jx--->Ih'
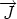Il reste à trouver ---> J pour que la base (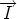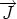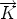---> I, ---> J, ---> K) soit directe : ---> J = ---> K × ---> I
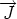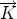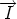
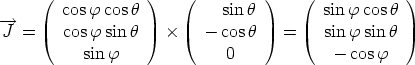
( ) ( ) ( ) ---> cosf cosh sin h sinf cos h J = cosf sinh × - cosh = sin fsin h sinf 0 - cosf
La matrice de transformation :
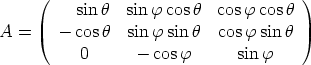
( ) sin h sinf cos h cosf cosh A = - cosh sinf sinh cosf sin h 0 - cosf sinf
permet de déterminer les coordonnées (x, y, z) d’un point M si on connaît ses coordonnées (X, Y, Z) dans le repère (O, ---> I, ---> J, ---> K).
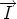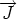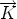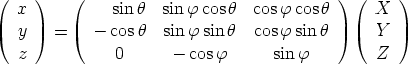
( x ) ( sin h sin f cosh cosf cos h ) ( X ) y = - cos h sin f sin h cos fsin h Y z 0 - cos f sin f Z
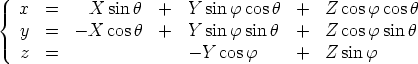
{ x = X sin h + Y sinf cosh + Z cosf cos h y = -X cosh + Y sinf sinh + Z cosf sinh z = - Y cosf + Z sinf
Si l’on considère un point du plan appartenant au plan XOY (Z = 0):
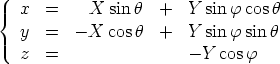
x = X sin h + Y sin f cosh { y = - X cos h + Y sin f sin h z = -Y cos f
Et si maintenant, ce repère OXY Z est translaté en un point O'(x O' , yO' , zO' )
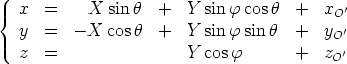
x = X sinh + Y sinf cos h + x ' { O y = - X cos h + Y sinf sinh + yO' z = Y cos f + zO'
Ce sont ces formules que j’ai utilisées pour définir, les cercles et les rectangles.

Réalisé par Manuel Luque, avec pour la mise en page LATEX, PSTricks pour les schémas et TEX-4ht pour la conversion en page HTML.

Les sources : maths_boulemiroir.zip