La méthode de la bissection exposée ici, est adaptée de celle de R.DONY qu’il développe dans son livre Graphisme scientifique sur micro-ordinateur publié chez Masson 1984/1985, aux pages 112,113,114,115,116 et 117. C’est un livre remarquable que je conseille à tous ceux qui souhaitent justement, s’initier aux graphismes 2D et 3D.
Nous nous limitons à la recherche d’une racine simple. La première démarche consiste à déterminer l’intervalle [x1,x2] où se trouve la racine. Une méthode rudimentaire consiste à tracer la fonction étudiée. L’exemple choisi sera très simple et les racines évidentes, ceci pour permettre une vérification aisée.
J’ai donc écrit trois commandes, qui vont être détaillées par la suite :
Les explications ci-dessous sont extraites du livre de R.DONY.
Le choix de l’équation : elle sera définie dans une variable \Function par :
\newcommand\Function{x x 0.6 sub mul x 2.3 sub mul x 3.5 sub mul x 4 sub mul}
|
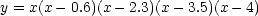
L’intervalle choisi est volontairement large [x1 = 0.8,x2 = 3].
«À chaque étape, l’intervalle étant divisé par deux, au bout de 10 itérations, l’intervalle initial sera réduit dans un facteur de 210 !
1 {
2 /XM X1 X2 add 2 div def % abscisse du milieu
3 /x X1 def
4 /Y1 Function def % valeur de la fonction Y1=y(x) pour x=X1
5 /x XM def
6 /YM Function def % valeur de la fonction YM=y(XM) pour x=XM
7 YM 0 eq {exit} if % si y(XM)=0 la racine est XM
8 Y1 YM mul 0 ge {/X1 XM def}
9 {/X2 XM def}
10 ifelse
11 X1 X2 sub abs 1e-6 le {exit} if
12 } loop
Cette commande s’écrit \pNodeRacine(x1,x2){I}{\Function}.
\renewcommand\Function{x 4 exp 9 x 3 exp mul sub 2 x 2 exp mul sub 120 x mul add 130 sub}
|
Exemple que j’emprunte au livre de R.DONY, page 112.
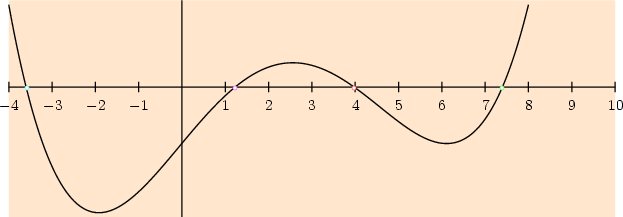
\begin{pspicture}(-4,-4)(10,2)
\psaxes[Dy=10](0,0)(-4,-4)(10,2) \psset{xunit=1,yunit=0.01} \psplot[plotpoints=200]{-4}{8}{\Function} \pNodeRacine(-5,-2){I}{\Function} \psdots[dotstyle=o,dotsize=1mm,linecolor=cyan](I) \pNodeRacine(0,2){I}{\Function} \psdots[dotstyle=o,dotsize=1mm,linecolor=magenta](I) \pNodeRacine(3,5){I}{\Function} \psdots[dotstyle=o,dotsize=1mm,linecolor=red](I) \pNodeRacine(6,8){I}{\Function} \psdots[dotstyle=o,dotsize=1mm,linecolor=green](I) \end{pspicture} |
Le cadre du dessin \begin{pspicture}(-4,-4)(10,2) doit être déterminé auparavant, on jouera aussi sur les échelles \psset{xunit=1,yunit=0.01}.
Elle s’utilise comme précédemment.
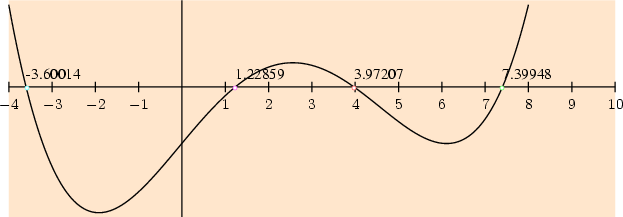
La racine comprise dans l'intervalle [-5,-2] vaut $x=\pNodeValeurRacine(-5,-2){I}{\Function}$
|
La racine comprise dans l’intervalle [-5,-2] vaut x =-3.60014
La racine comprise dans l’intervalle [0,2] vaut x =1.22859
La racine comprise dans l’intervalle [3,5] vaut x =3.97207
La racine comprise dans l’intervalle [6,8] vaut x =7.39948
Si l’on souhaite afficher la valeur de la racine au-dessus du point d’intersection, il suffit d’opérer ainsi :
\pNodeRacine(-5,-2){I}{\Function}
\psdots[dotstyle=o,dotsize=1mm,linecolor=cyan](I) \uput[90](I){\pNodeValeurRacine(-5,-2){I}{\Function}} |
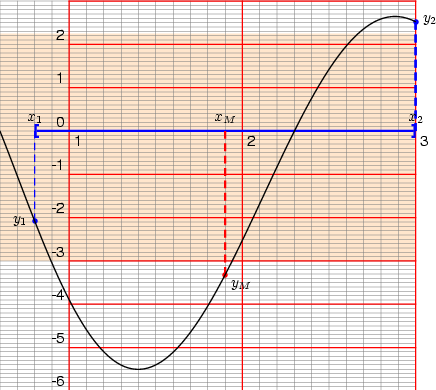
Il existe une commande dédiée à cela : \pNodeIteration. Elle s’utilise de la manière suivante :
\pNodeIteration[NbreIterations=0](0.8,3){I}{\Function}
|
[NbreIterations=0] permet de fixer le nombre d’itérations. L’intervalle s’affiche en rouge. L’intervalle initial est en bleu.
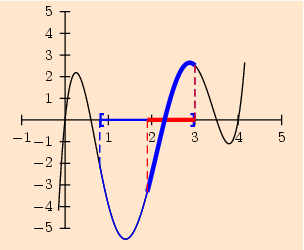
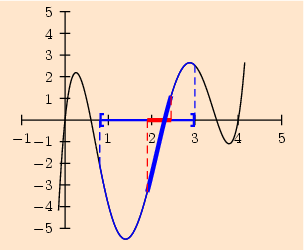
Une animation utilisant cette commande est visible sur la page Dichotomie_animation_png correspondante. On s’apercevra de la convergence très rapide de la méthode. L'ensemble des sources est disponible ici :
—