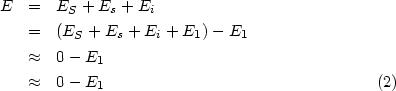Un extrait de l’interprétation du phénomène de la diffraction et du principe d’Huygens dans le cours de Berkeley, pages 480-482.

Figure 1 : des ondes planes émises par une source ponctuelle éloignée S tombent sur un écran opaque. La superposition due aux charges en S, s et i et sur le couvercle 1 crée un champ nul derrière l'écran.
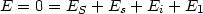
Trou dans un écran opaque. Faisons maintenant un petit trou (ou une petite fente) dans notre écran opaque. Créons d'abord la fente numéro 1 et appelons le matériau, dont elle a été constituée et que nous enlevons, le couvercle numéro 1. La partie de l'écran située respectivement au-dessus et en dessous du couvercle 1 est appelée s (supérieur) et i (inférieur). Le champ total derrière l'écran, qui est nul, est la superposition des champs émis par la source S et par les matériaux formant s, i, et le couvercle 1. Donc, avant d'avoir ôté la partie correspondant à la fente 1, nous avons
(1)

comme le montre la Fig.1.

Ôtons maintenant de l'écran le matériau qui constitue le couvercle 1. Supposons que le mouvement des électrons dans les régions s et i n'est pas modifié. (Ceci est une approximation, puisque les électrons des régions s et i sont excités par le champ électrique total qu'ils voient et que ce champ inclut le rayonnement des électrons contenus dans le couvercle. Les électrons de s et i peu éloignés du bord de la fente, c'est-à-dire de quelques longueurs d'onde, seront fortement affectés lorsqu'on enlèvera le couvercle, car le rayonnement d'un électron donné décroît lorsque la distance croît, si bien que les plus proches voisins ont la contribution la plus forte.)

Admettant néanmoins cette hypothèse, le champ total derrière l'écran n'est plus la superposition de l'Éq. (1), il est maintenant représenté par tous ses termes moins la contribution du couvercle 1 :

Nous voyons que le champ restant, qui est une superposition des contributions de la source S et du reste de l'écran s et i, est exactement (au signe près) le même que celui qui était émis lorsque le couvercle était en place. Nous pouvons donc calculer le champ situé derrière l'écran en imaginant que nous remplaçons la source et l'écran fendu par un système plus simple constitué du couvercle sans source S ni écran, tous les électrons du couvercle oscillant avec une amplitude et une phase égale, comme ils le faisaient lorsque le couvercle était en place. Voici un moyen simple de calculer la figure d'interférence due à une fente faite dans un écran opaque. La méthode est commode, car il est ici inutile de connaître la variation de l'amplitude et de la phase des électrons oscillant dans le couvercle suivant leur position dans la direction du faisceau (puisque bien entendu l'écran a une épaisseur finie). Si ceci était connu, nous pourrions étudier également le rayonnement vers l'arrière du couvercle et nous serions capables de distinguer entre un écran réfléchissant et un écran noirci. Pour l'instant, nous nous contenterons de supposer que le champ E1 créé par le couvercle est dû à une couche infiniment mince de charges oscillant toutes en phase et avec la même amplitude.

Principe d'Huygens. Il peut être utilisé quel que soit le nombre de fentes ou leur largeur; il est basé sur les Éqs. (1) et (2). Remarquez que l'artifice consistant à utiliser un couvercle rayonnant ne nous fournit la figure d'interférence correcte qu'en se plaçant derrière l'écran. Un véritable couvercle rayonnant, c'est-à-dire une antenne, rayonne dans toutes les directions. Un véritable écran opaque percé d'un trou présente une certaine quantité de rayonnement vers l'arrière, selon qu'il est réfléchissant ou opaque. Le couvercle de Huygens ne peut être utilisé pour calculer le champ à gauche de l'écran (supposant que le rayonnement incident provient de la gauche, comme c'est le cas sur la figure), car nous y négligeons les variations d'amplitude et de phase qui se produisent entre les surfaces avant et arrière du couvercle. Ces variations dépendent de l'état de surface de celui-ci : réfléchissant ou noir.

Il nous faut également remarquer qu'en écrivant l'Éq. (2), nous avons supposé que Es, et Ei ne dépendaient pas de la présence ou de l'absence du couvercle. Ceci, comme nous l'avons déjà souligné, n'est que partiellement vrai. Dans le cas, par exemple, d'une seule fente large, on pourrait utiliser la construction d'Huygens pour calculer les champs à droite de l'écran et dans la fente : si l'on est suffisamment à droite de l'écran et si ce dernier a une hauteur égale à un grand nombre de longueurs d'onde, la construction d'Huygens nous fournit une réponse pratiquement correcte (comme on peut le vérifier expérimentalement). Si l'on est au voisinage de la fente, la construction d'Huygens donne une approximation médiocre du résultat réel. En se plaçant à l'intérieur de la fente, les charges dont le mouvement contribue le plus au champ sont celles de l'écran qui se trouvent près des bords de la fente. Mais ce sont justement ces dernières dont le mouvement a subi le contrecoup de l'enlèvement du couvercle. L'aspect du champ peut être extrêmement compliqué dans la fente, et tout particulièrement près de ses bords où domine l'effet des charges les plus proches. Vous pourriez alors demander pour quelle raison on ne tente pas de résoudre exactement ce problème? En fait, le calcul est très difficile ; il faut utiliser les équations de Maxwell dans le vide et dans tous les matériaux, dont on spécifie exactement les propriétés, et résoudre ces équations en s'assurant que toutes les conditions aux limites sont vérifiées. Il n'y a aucune méthode générale pour calculer ces solutions et le calcul analytique exact n'est possible que dans un nombre très limité de cas. Le cours se poursuit, page 482 et suivantes par le calcul de la figure de diffraction d'une fente unique à l'aide de la construction d'Huygens.