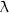 , serait le complément de son
inclinaison sur l’équateur ou de la distance du pôle à l’extrémité du diamètre
passant par le point de vue.
, serait le complément de son
inclinaison sur l’équateur ou de la distance du pôle à l’extrémité du diamètre
passant par le point de vue.
|
Résumé
Ces quelques exemples sont extraits du livre d’A. GERMAIN : Traité des projections des cartes géographiques, édité vers 1870 par Arthus BERTRAND à Paris. J’ai recopié intégralement les pages 111, 12 et 113 de son livre, la figure 21 a été numérisée à partir de son livre (je m’excuse de ne pas avoir eu la patience de la refaire avec PSTricks...avis aux amateurs !). Tous les autres schémas ont été réalisés avec le package pst-map3d. |
Les projections perspectives représentent la surface d’une sphère comme la verrait un spectateur placé en un point déterminé de l’espace ; la représentation de chaque point de la surface s’obtient par l’intersection du rayon visuel mené de l’œil à ce point, et d’un plan appelé tableau, perpendiculaire au rayon qui joint l’œil au centre ; une ligne quelconque tracée sur la surface a de même pour projection perspective l’intersection du plan du tableau avec la surface conique dont cette ligne est la directrice et le point de vue le sommet.
La distance du tableau au centre du globe ne fixant que l’échelle de la carte, peut rester arbitraire ; elle se détermine le plus souvent par de simples considérations de tracé graphique ; mais de la position du point de vue dépendent la forme et les propriétés de la projection, de sorte que cette position varie suivant le but qu’on se propose.
Remarquons d’abord que, quand le point le vue est situé dans l’intérieur de la sphère (ce qui est le cas d’un observateur regardant la voûte céleste), c’est la surface intérieure de la sphère que l’on représente. Il en est encore de même lorsque le point de vue est sur cette surface ou à une petite distance ; car, si l’on voulait représenter l’hémisphère antérieur, le rapprochement des rayons visuels dans le voisinage des tangentes extrêmes apporterait beaucoup de confusion dans le dessin et ne permettrait pas de représenter un hémisphère entier sans surcharger les bords de la carte. Mais dans le cas où l’œil est supposé à une distance du globe assez grande pour que les rayons visuels puissent être considérés comme parallèles, le même inconvénient n’existant plus, c’est la surface antérieure, celle que l’on voit réellement, qui doit être représentée.
L’une des principales propriétés de toute projection perspective, c’est que tout grand cercle passant par l’axe optique a pour projection un diamètre du cercle qui limite le tableau ; les autres cercles ont pour perspectives des courbes du second degré, puisque ce sont les sections planes de cônes ayant tous des cercles pour directrices.
Nous allons nous occuper de tracer le canevas, c’est-à-dire les méridiens et les parallèles d’une projection perspective. Cherchons d’abord les formules qui permettent de calculer les coordonnées d’un point défini par sa latitude et sa longitude.
Nous supposerons, dans tout ce qui va suivre, que le plan de projection coïncide avec l’un des grands cercles de la sphère ; dans le cas où il n’en serait pas ainsi, il suffirait, pour passer de ce plan fictif au plan réel auquel il est parallèle, de réduire toutes les lignes de la figure dans le rapport de la distance du point de vue au centre de la sphère, à la distance du point de vue au plan de projection. Enfin nous supposerons dans tout ce qui va suivre la terre sphérique, nous réservant d’indiquer, dans chaque système en particulier, la correction à faire pour tenir compte de l’aplatissement.
Le grand cercle de la sphère pris pour plan du tableau pourra être considéré
comme l’horizon d’un lieu dont la latitude 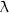 , serait le complément de son
inclinaison sur l’équateur ou de la distance du pôle à l’extrémité du diamètre
passant par le point de vue.
, serait le complément de son
inclinaison sur l’équateur ou de la distance du pôle à l’extrémité du diamètre
passant par le point de vue.
Prenons pour plan de la figure celui du méridien PzH'z'H' qui contient le point de vue V et est, par conséquent, perpendiculaire au plan du tableau HTH' ; nous supposerons les longitudes t comptées à partir de ce méridien, ce qui revient à ne considérer que les différences des longitudes de ce méridien et de tous ceux que l’on aura à construire sur la carte.
Prenons dans le plan du tableau deux axes de coordonnées, dont l’un sera l’intersection du méridien principal et du grand cercle de projection et dont l’autre passant par le centre C sera perpendiculaire au premier (fig. 21).
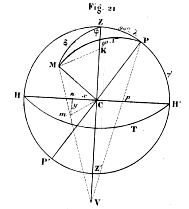
Appelons D est la distance donnée CV du centre de la sphère au point de vue V, a le
rayon de la sphère, 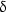 la distance angulaire Mz, 90o -
la distance angulaire Mz, 90o - 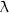 l’angle ZCP qui définit la
position du tableau, 90o - l la distance polaire du point considéré M, t sa
longitude ZPM,
l’angle ZCP qui définit la
position du tableau, 90o - l la distance polaire du point considéré M, t sa
longitude ZPM, 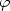 l’angle au zénith, MZP.
l’angle au zénith, MZP.
Une série de calculs, en particulier de trigonométrie sphérique, permettent à A. GERMAIN d’aboutir aux relations suivantes :
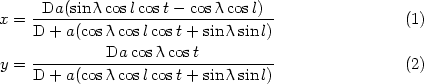
Si l’on suppose l’œil placé sur le prolongement de l’axe de la Terre, le plan de
projection coïncide avec l’équateur et la projection est dite équatoriale ou polaire.
Nous obtiendrons les valeurs de x et de y en faisant 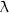 = 90o dans les formules (1)
et (2) page 113.
= 90o dans les formules (1)
et (2) page 113.
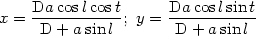
Si l’on suppose l’œil placé dans le plan de l’équateur, le plan de projection
coïncide avec un méridien et la projection est dite méridienne. Nous obtenons
alors les valeurs de x et de y en faisant 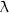 = 0 dans les formules (1) et (2)page
114.
= 0 dans les formules (1) et (2)page
114.
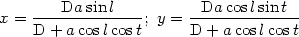
Le point de vue et le centre de la sphère coïncident, le plan de projection est reculé jusqu’à la surface de la sphère où il est tangent.
Lorsque le point de vue est sur la surface de la sphère, la projection prend le nom de stéréographique, et jouit de cette propriété remarquable que tout angle tracé sur la sphère conserve sa grandeur en projection, d’où il résulte que tout cercle a pour projection un autre cercle. Ce systèmepages 123/124, qui n’a reçu le nom de stéréographique qu’en 1643 du jésuite François d’AGUILLON, fut imaginé 130 ans avant J.-C. par le célèbre HIPPARQUE, qui lui donna le nom de planisphère[...]
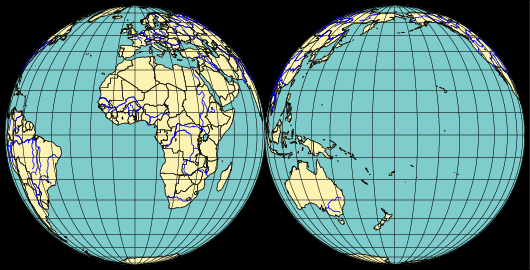
Si le point de vue est supposé à une distance infinie, les rayons visuels peuvent être regardés comme parallèles, la perspective devient une véritable projection orthogonale et prend le nom d’orthographiquepage 124 ; il en résulte que tout cercle parallèle au plan de projection a pour représentant un cercle égal. Imaginé comme le précédent par HIPPARQUE, ce système appelé primitivement analemme, puis astrolabe de Rojas (1551), est resté exclusivement renfermé dans le domaine de l’astronomie jusqu’à l’atlas sphéroïdal de Laguillermie publié en 1843[...]
En voici les représentations polaire, méridienne et horizontale réalisées avec le package pst-map3d, en prenant une distance observateur-centre très grande : Dobs=1e10
\begin{pspicture}(-5.2,-5.2)(15.2,5.2)
\psset{Dobs=1e10,Decran=1e10} \WorldMapThreeD[PHI=90,THETA=0]% \rput(10,0){% \WorldMapThreeD[PHI=-90,THETA=0]}% \end{pspicture} |
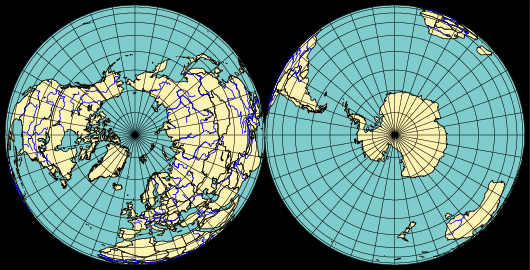
\begin{pspicture}(-5.2,-5.2)(15.2,5.2)
\psset{Dobs=1e10,Decran=1e10} \WorldMapThreeD[PHI=0,THETA=0]% \rput(10,0){% \WorldMapThreeD[PHI=0,THETA=180]}% \end{pspicture} |
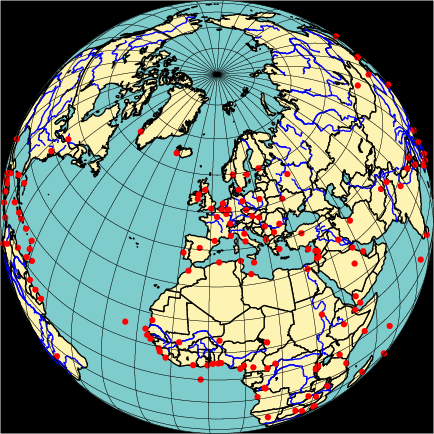
La projection sur l’horizon de Paris 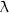 = 48,85o et L = 2,32o, donne :
= 48,85o et L = 2,32o, donne :
\begin{pspicture}(-5,-5)(5,5)
\psset{Dobs=1e10,Decran=1e10} \WorldMapThreeD[PHI=48.85,THETA=2.32,capital=true]% \end{pspicture} |
http://melusine.eu.org/syracuse/mluque/mappemonde/exemples-projections.zip
—