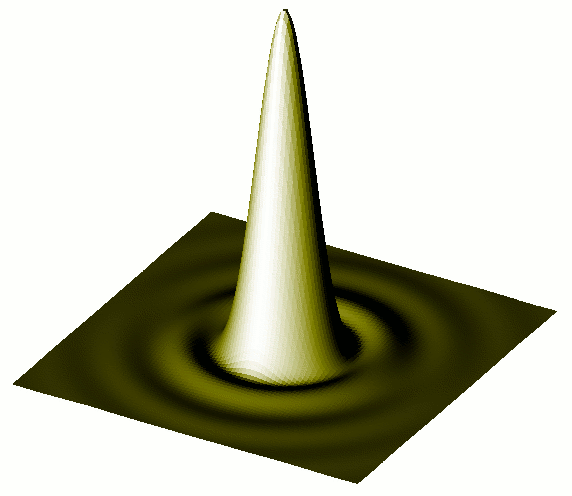
Ces solides de diffraction sont les surfaces en 3D : z = f(x,y), où z représente une grandeur proportionnelle à l'intensité lumineuse du point de l'écran de coordonnées (x,y).
Tous les calculs ont été faits en postscript, cela donne des fichiers assez compacts. La programmation n'a pas été optimisée et une réécriture plus rigoureuse permettrait d'améliorer grandement la vitesse d'affichage. Les exemples qui sont représentés sur cet écran sont des images au format gif, elles présentent un aspect crênelé sur les flancs montants qui n'existe pas dans les images au format ps lorsqu'on les imprime.
J'ai songé un moment de mettre ces fichiers dans des commandes PSTricks, afin d'avoir accés facilement aux divers paramètres, peut-être pour plus tard... Tous les paramètres sont facilement modifiables dans les fichiers ps. Je vais détailler dans chaque cas le moyen de le faire. Si on souhaite inclure l'une de ces images dans un fichier LaTeX, il suffit de la transformer au format eps.

|
| Figure 1 : solide de diffraction par un trou circulaire. |
/lambda 632 def % en nm
/r 1e-3 def % rayon de l'ouverture en m
/f 10 def % focale en m
THE 90 def
/PHE 10 def
/TH 30 def
/PH 30 def
/nbDiv 100 def
% les couleurs de base
/Cyan 0 def
/Magenta 0 def
/Yellow 1 def
/K 1 def
On peut donc choisir une autre couleur de départ, en se rappelant que ces valeurs sont comprises enre 0 et 1.
Cette couleur va être modifiée en fonction de l'inclinaison de la facette par rapport à la direction des rayons de la source de lumière et ce qui va suggérer l'effet de relief.
Dernier point, on peut dessiner les lignes à x constant, en décommentant les lignes suivantes :%R_limite neg pasLignes R_limite { % balayage suivant y
%/y exch def
% XE YE lineto
% } for
%1 0 1 0.5 setcmykcolor
%stroke
R_limite neg pasLignes R_limite { % balayage suivant y
/y exch def
XE YE lineto
} for
1 0 1 0.5 setcmykcolor
stroke
1 0 1 0.5 setcmykcolor
|
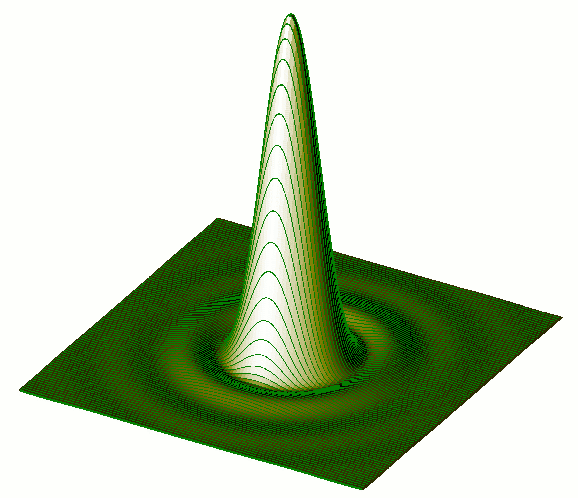
| Figure 1-bis : solide de diffraction par un trou circulaire avec lignes. |
CompteurLignes 3 mod 0 eq {
|
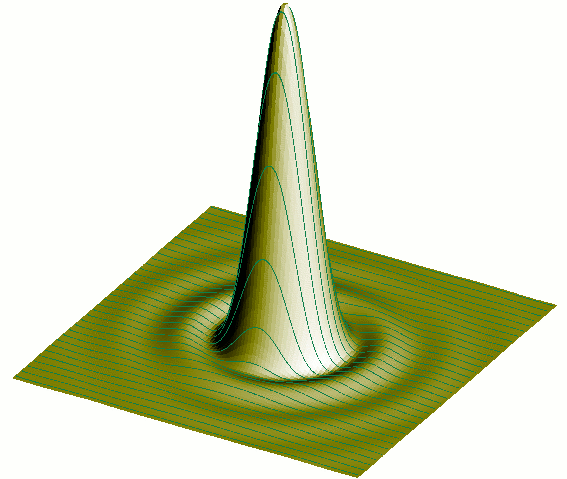
| Figure 1-ter : solide de diffraction par un trou circulaire avec 1 ligne sur 3. |
/echelle {2 mul} def

|
| Figure 2 : solide de diffraction par deux trous circulaires. |
/lambda 632 def % en nm
/r 1e-3 def % rayon du diamètre des trous, en m
/f 10 def % focale en m
/d {4 r mul} bind def % distance entre les centres des deux trous (d=4r)
|
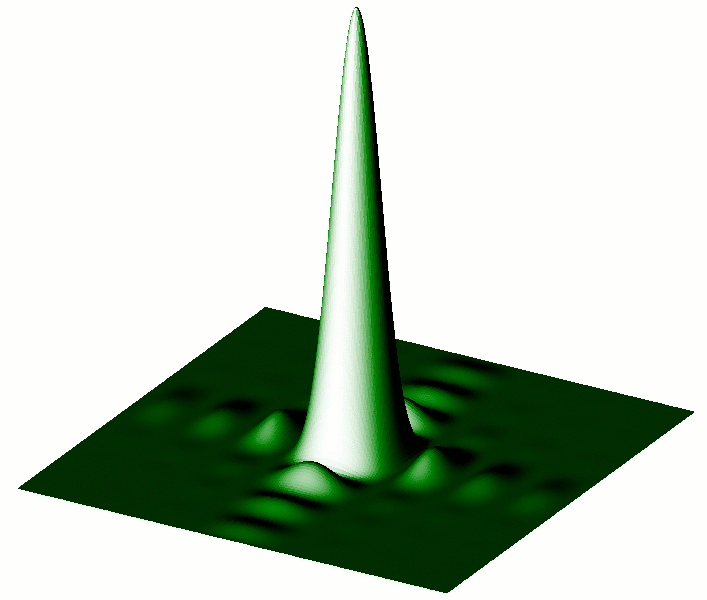
| Figure 3 : solide de diffraction par un trou rectangulaire. |
/lambda 632 def % en nm
/l 0.5e-3 def % largeur en m
/h 0.5e-3 def % hauteur en m
/f 10 def % focale en m
Peut-être prochainement y ajouterai-je, les représentations des différentes fonctions utilisées (Fresnel, Bessel), ainsi que la spirale de Cornu.
30 août 2004, modifié le 6 septembre 2004 : mluque5130@aol.com