$$\includegraphics{besancon1997.2}$$
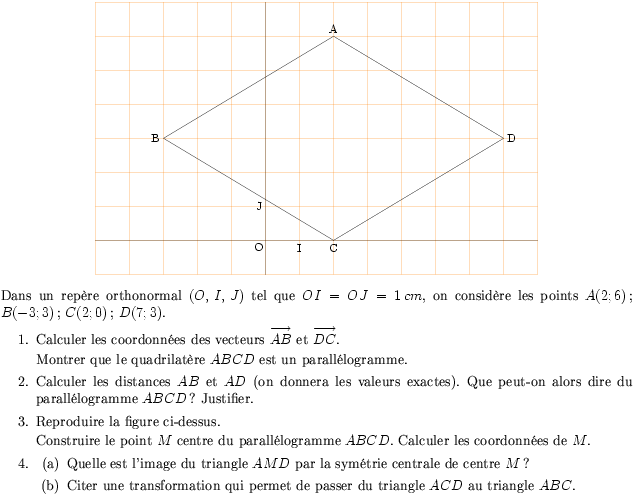
\par Dans un repère orthonormal $(O,\,I,\,J)$ tel que $OI=OJ=1\,cm$,
on considère les points $A(2; 6)$; $B(-3;3)$; $C(2; 0)$; $D(7; 3)$.
\begin{enumerate}
\item Calculer les coordonnées des vecteurs $\vecteur{\strut AB}$ et
$\vecteur{\strut DC}$.
\par Montrer que le quadrilatère $ABCD$ est un parallélogramme.
\item Calculer les distances $AB$ et $AD$ (on donnera les valeurs
exactes).  Que peut-on alors dire du parallélogramme $ABCD$?
Justifier.
\item Reproduire la figure ci-dessus.
\par Construire le point $M$ centre du parallélogramme
$ABCD$. Calculer les coordonnées de $M$.
\item
\begin{enumerate}
\item Quelle est l'image du triangle $AMD$ par la symétrie centrale de
centre $M$ ?
\item Citer une transformation qui permet de passer du triangle $ACD$
au triangle $ABC$.
\end{enumerate}
\end{enumerate}