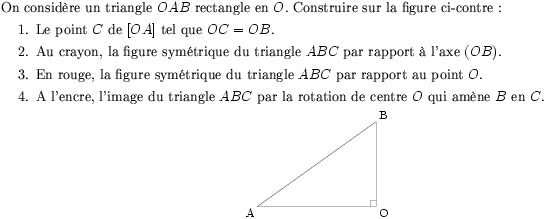
On considère un triangle $OAB$ rectangle en $O$. Construire sur la
figure ci-contre :
\begin{enumerate}
\item Le point $C$ de $[OA]$ tel que $OC=OB$.
\item Au crayon, la figure symétrique du triangle $ABC$ par rapport à
l'axe $(OB)$.
\item En rouge, la figure symétrique du triangle $ABC$ par rapport au
point $O$.
\item A l'encre, l'image du triangle $ABC$ par la rotation de centre
$O$ qui amène $B$ en $C$.
\end{enumerate}
$$\includegraphics{clermont1997.1}$$