\vspace*{2mm}
\paragraph{Deuxième Partie} : Etude de l'hexagone régulier.
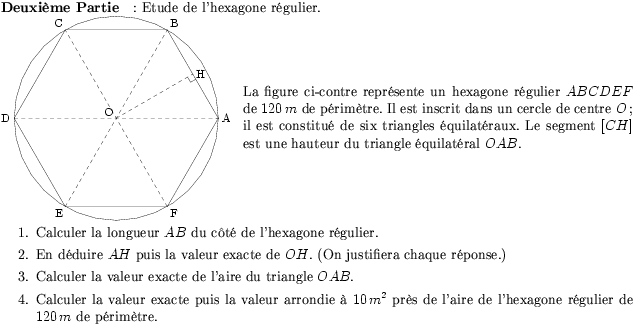
\par\compo{3}{clermont1997}{1}{La figure ci-contre représente un
hexagone régulier $ABCDEF$ de $120\,m$ de périmètre. Il est inscrit
dans un cercle de centre $O$; il est constitué de six triangles
équilatéraux. Le segment $[CH]$ est une hauteur du triangle
équilatéral $OAB$.}
\begin{enumerate}
\item Calculer la longueur $AB$ du côté de l'hexagone régulier.
\item En déduire $AH$ puis la valeur exacte de $OH$. (On justifiera
chaque réponse.)
\item Calculer la valeur exacte de l'aire du triangle $OAB$.
\item Calculer la valeur exacte puis la valeur arrondie à $10\,m^2$
près de l'aire de l'hexagone régulier de $120\,m$ de périmètre.
\end{enumerate}