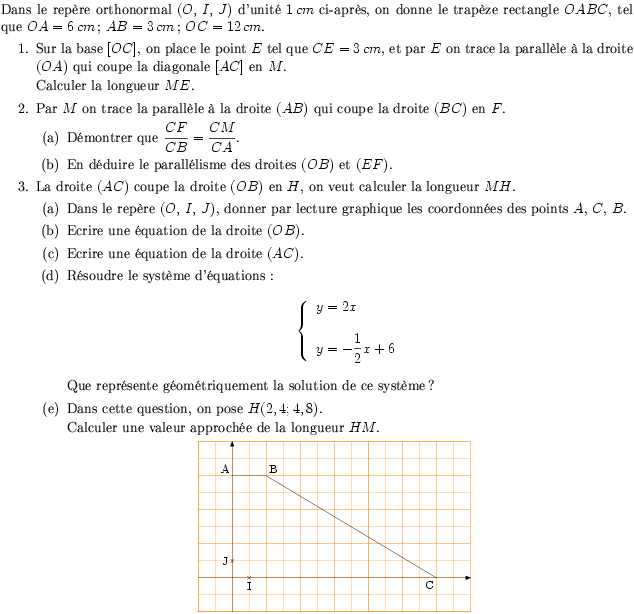
Dans le repère orthonormal $(O,\,I,\,J)$ d'unité $1\,cm$ ci-après, on
donne le trapèze rectangle $OABC$, tel que $OA=6\,cm$; $AB=3\,cm$;
$OC=12\,cm$.
\begin{enumerate}
\item Sur la base $[OC]$, on place le point $E$ tel que $CE = 3\,cm$,
et par $E$ on trace la parallèle à la droite $(OA)$ qui coupe la
diagonale $[AC]$ en $M$.
\par Calculer la longueur $ME$.
\item Par $M$ on trace la parallèle à la droite $(AB)$ qui coupe la
droite $(BC)$ en $F$.
\begin{enumerate}
\item Démontrer que $\dfrac{CF}{CB}=\dfrac{CM}{CA}$.
\item En déduire le parallélisme des droites $(OB)$ et $(EF)$.
\end{enumerate}
\item La droite $(AC)$ coupe la droite $(OB)$ en $H$, on veut calculer
la longueur $MH$.
\begin{enumerate}
\item Dans le repère $(O,\,I,\,J)$, donner par lecture graphique les
coordonnées des points $A$, $C$, $B$.
\item Ecrire une équation de la droite $(OB)$.
\item Ecrire une équation de la droite $(AC)$.
\item Résoudre le système d'équations :
$$\left\{\begin{tabular}{l}
$y=2x$\\
\\
$y=-\dfrac{1}{2}x+6$\\
\end{tabular}
\right.
$$
\par Que représente géométriquement la solution de ce système?
\item Dans cette question, on pose $H(2,4;4,8)$.\par Calculer une
valeur approchée de la longueur $HM$.
\end{enumerate}
$$\includegraphics{limoges1997.3}$$
\end{enumerate}