
$$\includegraphics{poitiers1997.1}$$
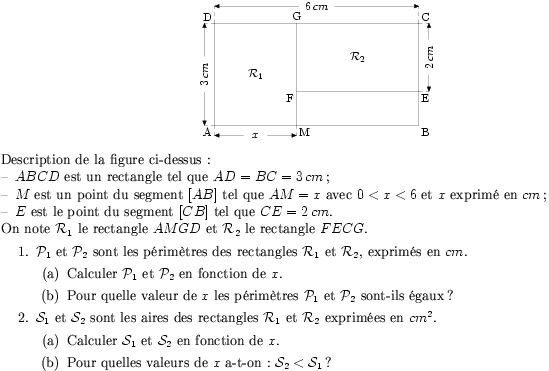
Description de la figure ci-dessus :
\begin{itemize}
\item $ABCD$ est un rectangle tel que $AD=BC=3\,cm$;
\item $M$ est un point du segment $[AB]$ tel que $AM=x$ avec $0<x<6$
et $x$ exprimé en $cm$;
\item $E$ est le point du segment $[CB]$ tel que $CE=2\,cm$.
\end{itemize}
\par On note ${\cal R}_1$ le rectangle $AMGD$ et ${\cal R}_2$ le
rectangle $FECG$.
\begin{enumerate}
\item ${\cal P}_1$ et ${\cal P}_2$ sont les périmètres des rectangles
${\cal R}_1$ et ${\cal R}_2$, exprimés en $cm$.
\begin{enumerate}
\item Calculer ${\cal P}_1$ et ${\cal P}_2$ en fonction de $x$.
\item Pour quelle valeur de $x$ les périmètres ${\cal P}_1$ et ${\cal
P}_2$ sont-ils égaux ?
\end{enumerate}
\item ${\cal S}_1$ et ${\cal S}_2$ sont les aires des rectangles
${\cal R}_1$ et ${\cal R}_2$ exprimées en $cm^2$.
\begin{enumerate}
\item Calculer ${\cal S}_1$ et ${\cal S}_2$ en fonction de $x$.
\item Pour quelles valeurs de $x$ a-t-on : ${\cal S}_2 < {\cal S}_1$?
\end{enumerate}
\end{enumerate}
|
