\begin{center}
\textbf{\Large{Partie B }}
\end{center}

Dans cette partie, on ne connaît pas la profondeur $SB$ de l'appentis.

Monsieur Ferdinand désire que :
\begin{itemize}
\item le volume de son appentis soit supérieur à $8m^3$ ;
\item la hauteur minimale $AB$ de son appentis soit supérieure à $1,60m$.
\end{itemize}
On désignera par $x$ la longueur de $[SB]$ exprimée en mètre. On utilisera : $OS=3,6m$.
\begin{enumerate}
\item Exprimer $OB$ en fonction de $x$.
\item Montrer, en utilisant le théorème de Thalès, que $AB=3-\dfrac{x}{1,2}$.
\item Résoudre l'inéquation : $3-\dfrac{x}{1,2} > 1,6$.
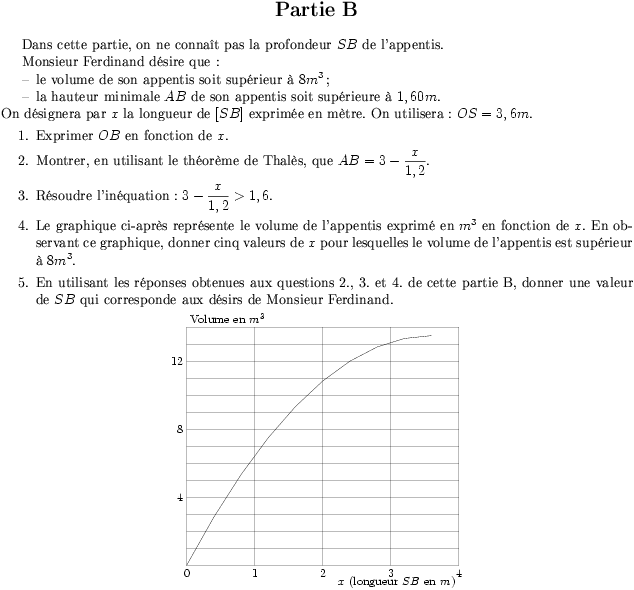
\item Le graphique ci-après représente le volume de l'appentis exprimé
en $m^3$ en fonction de $x$. En observant ce graphique, donner cinq
valeurs de $x$ pour lesquelles le volume de l'appentis est supérieur à
$8m^3$.
\item En utilisant les réponses obtenues aux questions 2., 3. et 4. de
cette partie B, donner une valeur de $SB$ qui corresponde aux désirs
de Monsieur Ferdinand.
\end{enumerate}
$$\includegraphics{centresetrangers12000.4}$$