\compo{1}{centresetrangers32000}{1}
{On rappelle que si l'aire de la base $\cal{B}$ et la hauyeur $h$, le
volume d'un cône est $\dfrac{1}{3} \cal{B} \times h$, et que le volume
d'une boule de rayon $r$ est $\dfrac{4}{3} \pi r^3$.

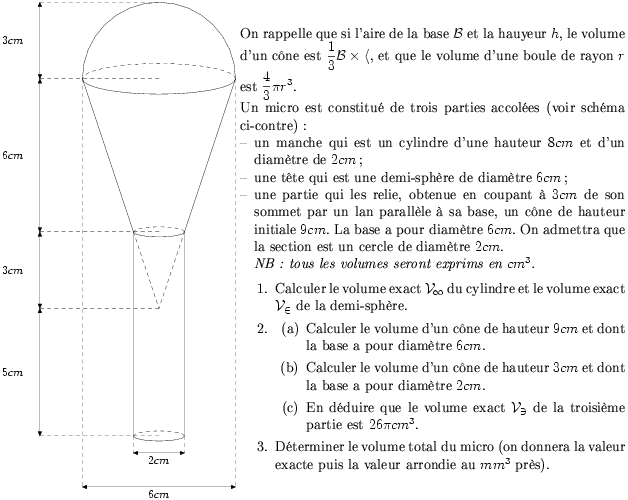
Un micro est constitué de trois parties accolées (voir schéma ci-contre) :
\begin{itemize}
\item un manche qui est un cylindre d'une hauteur $8cm$ et d'un diamètre de $2cm$ ;
\item une tête qui est une demi-sphère de diamètre $6cm$ ;
\item une partie qui les relie, obtenue en coupant à $3cm$ de son
sommet par un lan parallèle à sa base, un cône de hauteur initiale
$9cm$. La base a pour diamètre $6cm$. On admettra que la section est
un cercle de diamètre $2cm$.

\textit{NB : tous les volumes seront exprims en $cm^3$.}
\end{itemize}
\begin{enumerate}
\item Calculer le volume exact $\cal{V}_1$ du cylindre et le volume
exact $\cal{V}_2$ de la demi-sphère.
\item
\begin{enumerate}
\item Calculer le volume d'un cône de hauteur $9cm$ et dont la base a
pour diamètre $6cm$.
\item Calculer le volume d'un cône de hauteur $3cm$ et dont la base a
pour diamètre $2cm$.
\item En déduire que le volume exact $\cal{V}_3$ de la troisième
partie est $26 \pi cm^3$.
\end{enumerate}
\item Déterminer le volume total du micro (on donnera la valeur exacte
puis la valeur arrondie au $mm^3$ près).
\end{enumerate}
}