\textbf{Les deux parties peuvent être traitées de manière indépendante.}
\\Un artisan fabrique des boîtes en forme de tronc de pyramide pour un
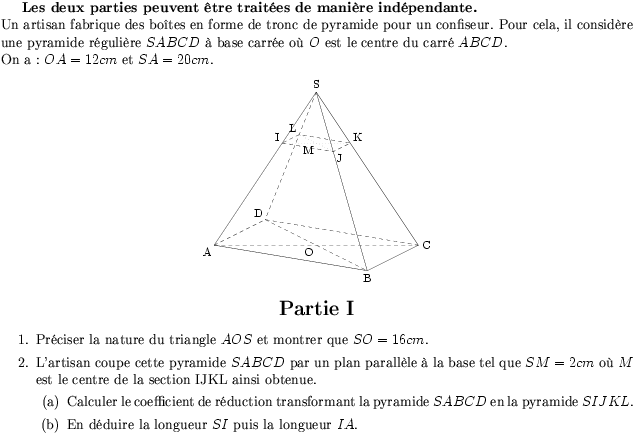
confiseur. Pour cela, il considère une pyramide régulière $SABCD$ à
base carrée où $O$ est le centre du carré $ABCD$.
\\On a : $OA=12cm$ et $SA=20cm$.
$$\includegraphics{afrique1-2002.2}$$
\begin{center}
\textbf{\Large{Partie I}}
\end{center}
\begin{enumerate}
\item Préciser la nature du triangle $AOS$ et montrer que $SO=16cm$.
\item L'artisan coupe cette pyramide $SABCD$ par un plan parallèle à
la base tel que $SM=2cm$ où $M$ est le centre de la section IJKL ainsi
obtenue.
\begin{enumerate}
\item Calculer le coefficient de réduction transformant la pyramide $SABCD$ en la pyramide $SIJKL$.
\item En déduire la longueur $SI$ puis la longueur $IA$.
\end{enumerate}
\end{enumerate}