\begin{center}
\textbf{\Large{Partie B}}
\end{center}
Dans cette partie le point $M$ n'est plus fixe mais \textbf{mobile}
sur le segment $[EF]$.
\\On pose $EM=x$ et ce nombre $x$ représente alors une
\textbf{longueur variable}.
\\(Il n'est pas demandé de nouvelle figure.)
\begin{enumerate}
\item
\begin{enumerate}
\item Entre quelles valeurs extrêmes peut varier le nombre $x$ ?
Soit $N$ le point de $[EG]$ défini comme dans la partie A.
\\Exprimer la longueur $EN$ en fonction de $x$.
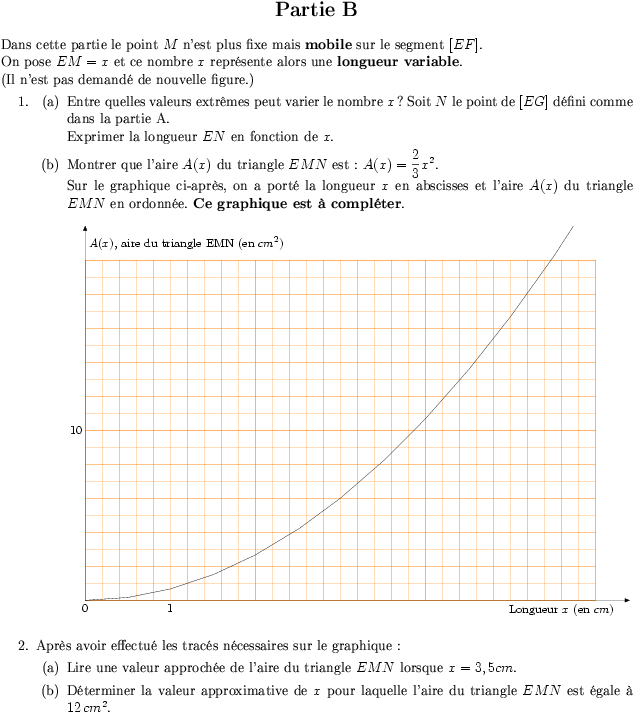
\item Montrer que l'aire $A(x)$ du triangle $EMN$ est :
$A(x)=\dfrac{2}{3}x^{2}$.
\\Sur le graphique ci-après, on a porté la longueur $x$ en abscisses
et l'aire $A(x)$ du triangle $EMN$ en ordonnée. \textbf{Ce graphique
est à compléter}.
$$ \includegraphics{afrique2-2002.3}$$
\end{enumerate}
\item Après avoir effectué les tracés nécessaires sur le graphique :
\begin{enumerate}
\item Lire une valeur approchée de l'aire du triangle $EMN$ lorsque
$x=3,5cm$.
\item Déterminer la valeur approximative de $x$ pour laquelle l'aire
du triangle $EMN$ est égale à $12\,cm^2$.
\end{enumerate}
\end{enumerate}