\textbf{Les constructions demandées dans cet exercice sont à réaliser
sur la figure suivante. Laisser les traces de construction visibles.}

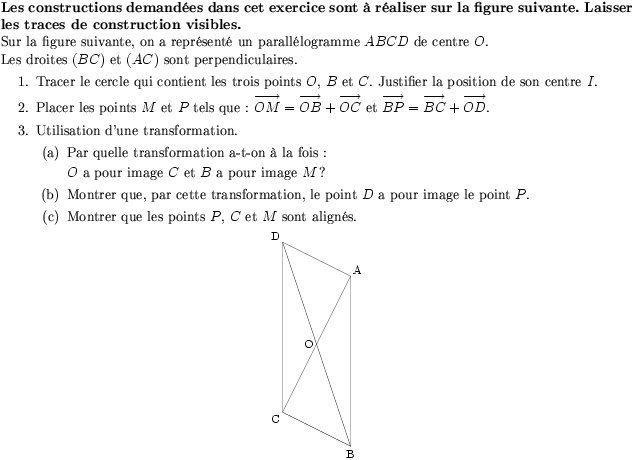
Sur la figure suivante, on a représenté un parallélogramme $ABCD$ de centre $O$.

Les droites $(BC)$ et $(AC)$ sont perpendiculaires.
\begin{enumerate}
\item Tracer le cercle qui contient les trois points $O$, $B$ et
$C$. Justifier la position de son centre $I$.
\item Placer les points $M$ et $P$ tels que :
$\overrightarrow{\strut OM}=\overrightarrow{\strut
OB}+\overrightarrow{\strut OC}$ et $\overrightarrow{\strut
BP}=\overrightarrow{\strut BC}+\overrightarrow{\strut OD}$.
\item Utilisation d'une transformation.
\begin{enumerate}
\item Par quelle transformation a-t-on à la fois :

$O$ a pour image $C$ et $B$ a pour image $M$ ?
\item Montrer que, par cette transformation, le point $D$ a pour image
le point $P$.
\item Montrer que les points $P$, $C$ et $M$ sont alignés.
\end{enumerate}
\end{enumerate}
$$\includegraphics{estlyon2002.2}$$