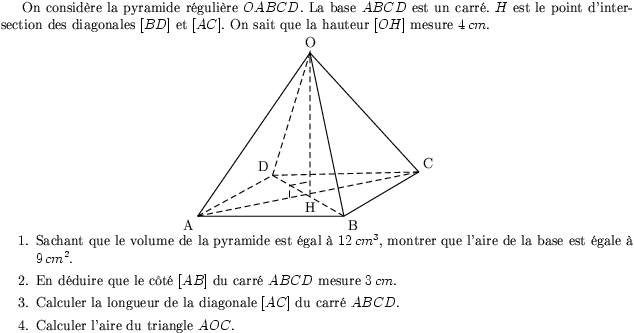
On considère la pyramide régulière $OABCD$. La base $ABCD$ est un
 carré.  $H$ est le point d'intersection des diagonales $[BD]$ et
 $[AC]$. On sait que la hauteur $[OH]$ mesure $4\,cm$.
\begin{center} \begin{pspicture}(7,5)
\uput[dl](0,0){A} \uput[dr](4.3,0){B}
\uput[ur](6.5,1.3){C} \uput[ul](2.2,1.2){D}
\uput[d](3.3,0.6){H} \uput[u](3.3,4.8){O}
\psline(0,0)(4.3,0)(6.5,1.3)(3.3,4.8)(4.3,0)%ABCOB
\psline(0,0)(3.3,4.8)%AO
\psline[linestyle=dashed](6.5,1.3)(2.2,1.2)%CD
\psline[linestyle=dashed](0,0)(6.5,1.3)%AC
\psline[linestyle=dashed](0,0)(2.2,1.2)(3.3,4.8)(3.3,0.6)%ADOH
\psline[linestyle=dashed](4.3,0)(2.2,1.2)%BD
\psline[linestyle=dashed](3.2,1)(2.7,0.9)(2.7,0.55)
\end{pspicture}
\end{center}
\begin{enumerate}
\item Sachant que le volume de la pyramide est égal à $12\,cm^3$,
montrer que l'aire de la base est égale à $9\,cm^2$.
\item En déduire que le côté $[AB]$ du carré $ABCD$ mesure $3\,cm$.
\item Calculer la longueur de la diagonale $[AC]$ du carré $ABCD$.
\item Calculer l'aire du triangle $AOC$.
\end{enumerate}