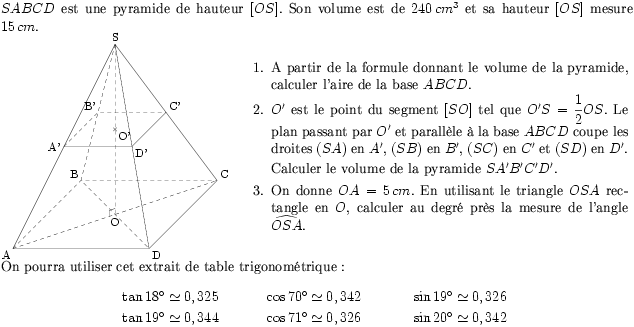
$SABCD$ est une pyramide de hauteur $[OS]$. Son volume est de
$240\,cm^3$ et sa hauteur $[OS]$ mesure $15\,cm$.
\par\compo{3}{lille1996}{1}{
\begin{enumerate}
\item A partir de la formule donnant le volume de la pyramide,
calculer l'aire de la base $ABCD$.
\item $O'$ est le point du segment $[SO]$ tel que
$O'S=\dfrac{1}{2}OS$. Le plan passant par $O'$ et parallèle à la base
$ABCD$ coupe les droites $(SA)$ en $A'$, $(SB)$ en $B'$, $(SC)$ en
$C'$ et $(SD)$ en $D'$.\par Calculer le volume de la pyramide
$SA'B'C'D'$.
\item On donne $OA=5\,cm$. En utilisant le triangle $OSA$ rectangle en
$O$, calculer au degré près la mesure de l'angle $\widehat{OSA}$.
\end{enumerate}
}
\par On pourra utiliser cet extrait de table trigonométrique :
$$\Eqalign{
\tan 18\mbox{°}&\simeq0,325\kern1cm&\cos
70\mbox{°}&\simeq0,342\kern1cm&\sin 19\mbox{°}&\simeq0,326\cr
\tan 19\mbox{°}&\simeq0,344&\cos 71\mbox{°}&\simeq0,326&\sin
20\mbox{°}&\simeq0,342\cr
}$$