comprendre.tex

 
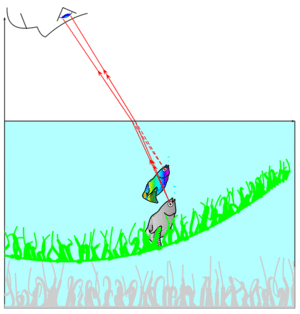
\documentclass{article}
\usepackage[T1]{fontenc}
\usepackage[garamond]{mathdesign}
\renewcommand{\ttdefault}{lmtt}
\usepackage[a4paper,dvips,hmargin=2cm,vmargin=3cm]{geometry}
\usepackage[colorlinks=true,dvips]{hyperref}
\usepackage[frenchb]{babel}
\usepackage{pst-slpe}
\usepackage{graphicx}
\usepackage{pst-grad}
\usepackage{framed}
\usepackage{pst-refraction}
 
\newcommand\Cadre[1]{\psframebox[fillstyle=solid,fillcolor=yellow,linecolor={[cmyk]{0,0,1,0.1}}]{\texttt{#1}}}
\newcommand\encadre[1]{\begin{center}
\psframebox[fillstyle=solid,fillcolor=green!33,linecolor=green,linewidth=0.5mm]{
  \begin{minipage}{0.95\textwidth}
  {#1}
  \end{minipage}}
  \end{center}}
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%% Jean-Michel Sarlat et Guillaume Connan
\newenvironment{gbar}{%
  \def\FrameCommand{{\color{red}\vrule width 2pt}\colorbox{yellow!30}}%
  \MakeFramed {\advance\hsize-\width \FrameRestore}}%
{\endMakeFramed}
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 
\input poissons.tex
\input mesange.tex
\input poisson_spectateur.tex
 
\makeatletter
% pour dessiner les herbes folles
\def\pNodeIrand{\@ifnextchar[{\pst@pNodeIrand}{\pst@pNodeIrand[]}}
\def\pst@pNodeIrand[#1](#2,#3)#4{{%
\pst@killglue
\psset{#1}%
\pnode(! %
 /xa #2 \psk@pstRefraction@xPos\space add rand sin 0.2 mul add def % valeur de xa abscisse réelle du point observé
 /ya #3 \psk@pstRefraction@yPos\space add rand sin 0.5 mul add def % valeur de ya ordonnée réelle du point observé <0 !
 /xb \psk@pstRefraction@xObservateur\space def % valeur de xb
 /yb \psk@pstRefraction@yObservateur\space def % valeur de yb
 /eyewidth \psk@pstRefraction@eyewidth\space def % dimension de l'oeil
 /xMilieu \psk@abscisseDirectionRegard\space def
% chercher B1 et B2 limites de l'oeil
 /DistanceYB1YB2 eyewidth xMilieu xb sub dup mul
      xMilieu xb sub dup mul yb dup mul add
      div sqrt mul def
 /yB1 yb DistanceYB1YB2 sub def
 /yB2 yb DistanceYB1YB2 add def
 /xB1 yb yB1 yb sub mul xMilieu xb sub div xb add def
 /xB2 yb yB2 yb sub mul xMilieu xb sub div xb add def
 /n \psk@pstRefraction@indice\space def % indice de l'eau
      tx@RefractionDict begin Coor_Virtuel end){#4}
}}
\makeatother
\title{De notre espace aérien, que voyons nous dans l'eau ?}
\begin{document}
\maketitle
\tableofcontents
\section{Présentation du problème}
Peut-être avez-vous le souvenir de vos premiers pas dans l'eau et de l'angoissante question que vous vous posiez : << jusqu'où puis-je avancer, est-ce que je vais avoir toujours pied si je vais un peu plus loin ? >>. Oui, les apparences sont trompeuses et le fond de l'eau apparaît plus près qu'il n'est en réalité, le poisson que l'on croit pouvoir attraper facilement est un peu plus loin qu'on l'imagine.
Les images des objets et des poissons qui sont dans l'eau et que nous observons depuis notre espace aérien nous apparaissent
différentes de ce qu'ils sont en réalité, ils nous semblent plus proches, plus petits, distordus, ce qui est en cause est le phénomène de la \Cadre{réfraction}. Le but de ce modeste article est d'essayer de comprendre ce phénomène.
 
Nous allons considérer dans une première étape un point lumineux
$A$ dans l'eau et un point $B$ dans l'air. Parmi tous les rayons
lumineux émis (ou diffusés) par ce point $A$, essayons de
déterminer la trajectoire du rayon qui après avoir traversé la
surface de l'eau passera par $B$. Ensuite, dans une deuxième étape
nous considérerons un objet ou un poisson dans l'eau et un
spectateur au-dessus de l'eau dont nous essayerons de reconstituer
l'image qu'il en perçoit. Pour terminer nous inverserons la situation, que peut voir un poisson qui regarde ce qui se passe de l'autre côté de la surface, dans l'espace aérien ?
\section{Le trajet d'un rayon lumineux}
\begin{center}
\begin{pspicture}(0,-5)(10.5,5.5)
\psset{xObservateur=2,yObservateur=4}
\psframe*[linecolor=eau](0,-5)(10,0)
\psline{->}(10.5,0)
\psline{->}(0,-5)(0,5.5)
\pNodeI(8,-4){V}
\pnode(! xa ya){A}
\pnode(! xI1 0){I1}
\pnode(! xB1 yB1){B1}
\pnode(! xB1 0){Q}
\pnode(! xa 0){P}
\psline[linestyle=dotted](! xI1 -5)(! xI1 5)
\psarc(I1){1}{90}{133}
\rput(I1){\uput[111.5](1;111.5){$i_2$}}
\psarc[doubleline=true](I1){1}{270}{302}
\rput(I1){\uput[286](1;286){$i_1$}}
\psline[linecolor=red](A)(I1)(B1)
\pcline[nodesepB=2cm,linecolor=red,arrowsize=0.2]{->}(A)(I1)
\pcline[nodesepB=2cm,linecolor=red,arrowsize=0.2]{->}(I1)(B1)
\psline[linestyle=dashed](B1)(Q)
\psline[linestyle=dashed](A)(P)
\uput[0](0,5.5){$y$}
\uput[0](10.5,0){$x$}
\uput[180](0,0){$O$}
\uput[45](I1){$I$}
\qdisk(A){1.5pt}
\uput[0](A){$A$}
\qdisk(B1){1.5pt}
\uput[90](B1){$B$}
\uput[-90](2,0){$Q$}
\uput[90](8,0){$P$}
\uput[u](9,0){$(\Pi)$}
%\psgrid
\end{pspicture}
\end{center}
Il s'agit de calculer les coordonnées du point d'intersection
$I(x_I,y_I)$ d'un rayon lumineux émis par un point $A(x_A,y_A)$ situé dans la
piscine avec la surface de l'eau, pour qu'après réfraction en $I$(le trajet du rayon suivant les lois de la réfraction de \textsc{Descartes} \Cadre{$n_1\sin i_1=n_2\sin i_2$}), ce rayon
parvienne au point $B(x_B,y_B)$ censé représenter un observateur.
 
On prendra $n_2=1$ pour l'air et $n_1=1.33$ pour l'eau. $i_1$ et
$i_2$ sont les angles mesurés par rapport à la normale.
\par
Les données sont donc $A(x_A,y_A)$ et $B(x_B,y_B)$. Il
s'agit de trouver $I(x_I,y_I)$.
 
\begin{gbar}
Si $P$ et $Q$ sont les projections
orthogonales de $A$ et $B$ sur la surface de l'eau $(\Pi)$, le point d'incidence $I$ appartient au segment $[PQ]$ :
 $$\overrightarrow{PI}=t\overrightarrow{PQ}\ \textrm{avec } t\in[0,1]$$
La figure précédente est dans le plan vertical passant par les points $A$ et $B$.
Le problème est donc de trouver $I$ aligné avec les projections
de $A$ et $B$ sur $(\Pi)$.
 $n=n_1/n_2$ est l'indice de l'eau par rapport à l'air. On peut modifier ce paramètre.
 \begin{equation}
 n\sin
 i_1=\frac{n|x_I-x_A|}{\sqrt{(x_I-x_A)^2+y_A^2}}=\frac{|x_I-x_B|}{\sqrt{(x_I-x_B)^2+y_B^2}}=\sin i_2
 \end{equation}
La racine de l'équation :
\begin{equation}
\frac{n|x_I-x_A|}{\sqrt{(x_I-x_A)^2+y_A^2}}-\frac{|x_I-x_B|}{\sqrt{(x_I-x_B)^2+y_B^2}}=0
 \end{equation}
comprise dans l'intervalle $[x_A,x_B]$ donne la solution du problème.
\end{gbar}
\section{La formation des images pour l'observateur}
On considère un point situé dans l'eau $A$ émettant des rayons lumineux dans toutes les directions et on isole, par la pensée, un mince pinceau lumineux qui après réfraction à la surface de l'eau pénètre par la pupille dans l'\oe{}il d'un observateur.
\begin{gbar}
L'\oe{}il ne << voit >> pas les lignes brisées et interprète les rayons qu'il reçoit comme
s'ils venaient tout droits. L'observateur voit $A'$ qui est l'image, \textit{virtuelle}, de $A$ par réfraction.
\end{gbar}
En appliquant ce principe à tous les points de l'objet observé, on peut reconstituer l'image totale. La position réelle est grisée, l'image observée est en couleurs.
 
\begin{center}
\begin{pspicture}(0,-9)(15,6)
\psframe*[linecolor=eau](0,-9)(14,0)
\psline{->}(14,0)
\psline{->}(0,-5)(0,5)
\psset{xObservateur=3,yObservateur=5,abscisseDirectionRegard=5}
\EyeDraw
\psset{xPos=8,yPos=-4}
{\psset{linewidth=0.02}\PoissonXY}
{\psset{linewidth=0.02}\RefractionPoissonTwo}
\pNodeI(0,0){V}
\pnode(! xa ya ){A}
%{\psset{linecolor=red}\qdisk(A){2pt}}
\pnode(! xb yb ){B}
\pnode(! xB1 yB1){B1}
\pnode(! xB2 yB2){B2}
\pnode(! xI1 0){I1}
\pnode(! xI2 0){I2}
\psline[linecolor=red](B1)(I1)(A)
\psline[linecolor=red](B2)(I2)(A)
\psset{arrowsize=0.2}
\pcline[nodesepB=2cm,linecolor=red]{->}(A)(I1)
\pcline[nodesepB=2cm,linecolor=red]{->>}(A)(I2)
\pcline[nodesepB=3cm,linecolor=red]{->}(I1)(B1)
\pcline[nodesepB=3cm,linecolor=red]{->>}(I2)(B2)
\psline[linestyle=dashed,linecolor=red](I2)(V)
\psline[linestyle=dashed,linecolor=red](I1)(V)
\psclip{\psframe(0,-9)(14,0)}
{\psset{linewidth=0.2,LineWidthStep=-0.07,linecolor=MonGris}
\psset{xPos=0,yPos=0}
\multido{\rX=0+0.25}{68}{%
  \pnode(! \rX\space -9){h1}
  \pnode(! \rX\space rand sin 0.2 mul add -8.5 rand sin 0.5 mul add ){h2}
  \pnode(! \rX\space rand sin 0.2 mul add -8 rand sin 0.5 mul add ){h3}
  \pnode(! \rX\space rand sin 0.2 mul add -7.5 rand sin 1 mul add ){h4}
  \PstCurveVaryingWidth(h1)(h2)(h3)(h4)}
\psline(0,-9)(15,-9)
\psset{linecolor=green}
\multido{\rX=0+0.25}{68}{%
  \pNodeI(\rX,-9){h1}
  \pNodeIrand(\rX, -8.5){h2}
  \pNodeIrand(\rX,-8){h3}
  \pNodeIrand(\rX,-7.5){h4}
  \PstCurveVaryingWidth(h1)(h2)(h3)(h4)}}
\psset{linecolor=green,linewidth=0.1}\RefractionPsline(0,-9)(15,-9)
\endpsclip
\end{pspicture}
\end{center}
\Cadre{``Tangente'' vue au travers de la réfraction.}
\begin{center}
\begin{pspicture}(0,-5)(10,6)
%\psframe(0,-5)(10,6)
%\psgrid
\psset{xObservateur=2,yObservateur=5,abscisseDirectionRegard=5}
\psframe*[linecolor=eau](0,-5)(10,0)
\EyeDraw
\psgrid[subgriddiv=0,gridlabels=0,gridcolor=red](0,-5)(10,-1)
\multido{\iY=-5+1}{5}{%
\RefractionPsline[linecolor=blue](0,\iY)(10,\iY)}
\multido{\iX=0+1}{11}{%
\RefractionPsline[linecolor=blue](\iX,-5)(\iX,-1)}
\textRefraction[fillstyle=solid,fillcolor=blue,linecolor=blue](4,-4){Tangente}
\rput(4,-4){\color{red}\fontfamily{ptm}\fontsize{56.90}{56.90}\selectfont Tangente}
%\psgrid
\end{pspicture}
\end{center}
\section{Comment un poisson perçoit notre univers ?}
Un essai de reconstitution de ce que verrait un poisson qui regarde au-delà de la surface de l'eau.
\begin{center}
\begin{pspicture}(0,-10)(15,7)
\psset{n=0.75}
\psframe*[linecolor=eau](0,-10)(15,0)
\psset{xObservateur=7,yObservateur=-5,eyewidth=0.10}
\pscircle*[linecolor=lightgray](10,2){1}
\RefractionPscircle[linecolor=blue,fillstyle=solid,fillcolor=CercleEau](10,2){1}
\EyePoisson
\RefractionPsline[linecolor=blue,linewidth=0.5mm](2,5)(13,5)(13,1)(2,1)(2,5)
\psline[linecolor=red,linewidth=0.5mm](2,5)(13,5)(13,1)(2,1)(2,5)
\psgrid[subgriddiv=0,gridlabels=0,gridcolor=red,gridwidth=0.2mm](2,5)(13,1)
\multido{\iY=5+-1}{5}{%
\RefractionPsline[linecolor=blue,linewidth=0.2mm](2,\iY)(13,\iY)}
\multido{\iX=2+1}{12}{%
\RefractionPsline[linecolor=blue,linewidth=0.2mm](\iX,5)(\iX,1)}
\pNodeI(13,5){V}
{\psset{linecolor=blue}\qdisk(V){2pt}}
\pnode(! xa ya ){A}
{\psset{linecolor=red}\qdisk(A){2pt}}
\pnode(! xb yb ){B}
\pnode(! xB1 yB1){B1}
\pnode(! xB2 yB2){B2}
\pnode(! xI1 0){I1}
\pnode(! xI2 0){I2}
\psline[linecolor=red](B1)(I1)(A)
\psline[linecolor=red](B2)(I2)(A)
\psset{arrowsize=0.2}
\pcline[nodesepB=2cm,linecolor=red]{->}(A)(I1)
\pcline[nodesepB=2cm,linecolor=red]{->>}(A)(I2)
\pcline[nodesepB=3cm,linecolor=red]{->}(I1)(B1)
\pcline[nodesepB=3cm,linecolor=red]{->>}(I2)(B2)
\psline[linestyle=dashed,linecolor=red](I2)(V)
\psline[linestyle=dashed,linecolor=red](I1)(V)
\Datas\ghostBranche\ghostMesange
\RefractionBranche\RefractionMesange
\psclip{\psframe(0,-10)(15,0)}
\psset{linewidth=0.2,LineWidthStep=-0.07,linecolor=green}
\multido{\rX=0+0.25}{68}{%
  \pnode(! \rX\space -10){h1}
  \pnode(! \rX\space rand sin 0.2 mul add -9.5 rand sin 0.5 mul add ){h2}
  \pnode(! \rX\space rand sin 0.2 mul add -9 rand sin 0.5 mul add ){h3}
  \pnode(! \rX\space rand sin 0.2 mul add -8.5 rand sin 1 mul add ){h4}
  \PstCurveVaryingWidth(h1)(h2)(h3)(h4)}
\endpsclip
\end{pspicture}
\end{center}
\end{document}