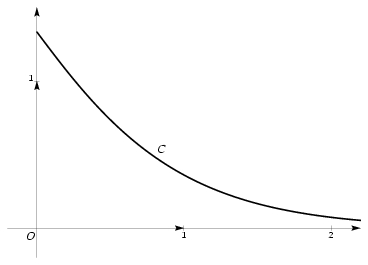
\exo {Une équation différentielle d'ordre 2} {\sl L'objectif de cet exercice est de résoudre une équation différentielle dont une solution particulière est susceptible de définir une fonction de densité en probabilités.} \medskip \centerline {\bf Les parties A. et B. peuvent être traitées de façon indépendante.} \medskip \let \partie \centerpartie \partie {A -- Résolution d'une équation différentielle} On considère l'équation différentielle $$ y''-4y = - {16\over 3} e^{-2x} \leqno (E) $$ où $y$ est une fonction de la variable réelle $x$, définie et deux fois dérivable sur $\rset $, $y'$ la fonction dérivée de $y$, et $y''$ sa fonction dérivée seconde. \itemnum Résoudre sur $\rset $ l'équation différentielle %%$(E_0)~: \quad y''-4y=0$. $$ y''-4y=0. \leqno (E_0) $$ \itemnum Vérifier que la fonction $g$ définie sur $\rset $ par $$ g (x) = {4\over 3} xe^{-2x} $$ est une solution particulière de l'équation différentielle $(E)$. \itemnum En déduire l'ensemble des solutions de l'équation différentielle $(E)$. \itemnum Déterminer la solution particulière $h$ de l'équation différentielle $(E)$ vérifiant les con\-di\-tions $$ h (0) = {4\over 3} \qquad {\rm et} \qquad h' (0) = -{4\over 3}. $$ \partie {B -- \' Etude d'une fonction} \def \epspath {} \epsfxsize 80mm Soit $f$ la fonction définie sur $[0, +\infty [$ par $$ f (x) = {4\over 3} (1+x) e^{-2x} $$ $$ \qquad \qquad \vcenter {\superboxepsillustrate {equ2_016.ps}} $$ Une représentation graphique $C$ de $f$, dans un repère orthogonal, est donnée ci-dessus. \itemnum Le graphique suggère un sens de variation pour la fonction $f$. L'objet de cette question est de justifier ce résultat. \itemitemalph Démontrer que, pour tout $x$ de $[0, +\infty [$, $$ f' (x) = -{4\over 3} (2x+1)e^{-2x}. $$ \itemitemalph En déduire le sens de variation de $f$ sur $[0, +\infty [$. \itemnum Le graphique permet d'envisager une asymptote en $+\infty $ pour la courbe $C$. \` A partir de l'expression de $f (x)$, déterminer une limite de $f$ justifiant cette propriété graphique. \itemitemalphnum \` A l'aide du développement limité au voisinage de~0 de la fonction exponentielle $t\mapsto e^t$, donner le développement limité à l'ordre~3 au voisinage de~0 de la fonction $x\mapsto e^{-2x}$. \itemitemalph En déduire que le développement limité à l'ordre~3 au voisinage de~0 de la fonction $f$ est~: $$ f (x) = {4\over 3} - {4\over 3}x + {8\over 9}x^3 + x^3 \varepsilon (x) \qquad {\rm avec} \quad \lim _{x\to 0} \varepsilon (x) = 0. $$ \itemitemalph En déduire une équation de la tangente $T$ à la courbe $C$ au point d'abscisse~0 et la position relative de $C$ et $t$, pour $x$ positif au voisinage de~0. \itemitemalphnum \` A l'aide d'une intégration par parties, calculer la valeur exacte de l'intégrale~; $$ I = \int _0^3 f (x) \, dx. $$ Donner une valeur approchée, arrondie au centième, de l'intégrale $I$. \itemitem {} Donner une interprétation graphique de l'intégrale $I$. \itemitemalph Sur l'écran d'une calculatrice, équipée d'un logiciel particulier (calcul formel), on lit le résultat suivant, où $t$ est un nombre réel positif quelconque~: $$ I = \int _0^t f (x) \, dx = \left( -{2\over 3} t - 1\right) e^{-2t} + 1. $$ {\bf Ce résultat est admis ici et n'a donc pas à être démontré.} \itemitem {} Déterminer $$ \lim _{t\to +\infty } \left( -{2\over 3} t - 1\right) e^{-2t}. $$ \itemitemalph Soit $A (t)$ l'aire, en unités d'aire, de la partie du plan limitée par les axes de coordonnées, la courbe $C$, et la droite d'équation $x=t$ où $t$ est un nombre réel positif. \itemitem {} Déterminer $\displaystyle {J = \lim _{t\to +\infty } A (t)}$. \itemitemalph Déterminer la valeur exacte de $J-I$ où $I = A (3)$ a été calculé à la question {\bf 4.}{\sl a\/}), et en déduire la double inégalité~: $0\leq J-I\leq 10^{-2}$. \itemitem {} Donner, à l'aide d'une phrase, une interprétation graphique de $J-I$. \finexo \corrige {} \let \partie \llappartie \partie {A} % \num \ L'équation caractéristique associée à $(E_0)$ est l'équation $r^2 - 4 = 0$, quiadmet les 2~racines réelles $r_1 = 2$. et $r_2 = -2$. Le cours nous dit alors que les solutions de $(E_0)$ sont toutes les fonctions $y$ ayant une écriture de la forme $$\dresultat { y (x) = A e^{2x} + Be^{-2x} \qquad {\rm où} \qquad \hbox {$A$ et $B$ sont 2 constantes réelles quelconques} }$$ \num \ \` A partir de la fonction $g$ donnée, on trouve $$ g (x) = {4\over 3} xe^{-2x} \qquad \qquad g' (x) = {4\over 3} (-2x+1) e^{-2x} \qquad {\rm et} \qquad g'' (x) = {16\over 3} (x-1) e^{-2x} $$ Il est alors facile de vérifier que l'on a bien $$ g''-4g = - {16\over 3} e^{-2x} $$ autrement dit que l'on a bien \tresultat {$g$ solution particulière de $(E)$}. \num \ On sait que la solution générale de $(E)$ est obtenue en additionnant une solution particulière de $(E)$ et la solution générale de $(E_0)$. Ici on obtient comme solution générale de $(E)$ la fonction $y$ définie par $$\dresultat { y (x) = {4\over 3} xe^{-2x} + A e^{2x} + Be^{-2x} \qquad {\rm où} \qquad \hbox {$A$ et $B$ sont 2 constantes réelles quelconques} }$$ \num \ Soit $h$ une solution de $(E)$, on a alors $$ h' (x) = {4\over 3} (-2x+1) e^{-2x} +2Ae^{2x} - 2Be^{-2x} $$ ce qui donne $$ h (0) = A+B \qquad {\rm et} \qquad h' (0) = {4\over 3} + 2A -2B $$ Les conditions initiales imposées se traduisent alors par les 2~équations $$ A+B = {4\over 3} \qquad {\rm et} \qquad {4\over 3} + 2A -2B = -{4\over 3} \quad {\rm soit} \quad A -B = -{4\over 3} $$ d'où le système de 2~équations à 2~inconnues $$ \cases { A+B = 4/3 \cr A-B = -4/3 \cr } \qquad \hbox {dont l'unique solution est le couple} \qquad (A, B) = \left( 0, {4\over 3} \right) $$ Finalement, la seule fonction $h$ qui soit solution de l'équation différentielle $(E)$ tout en vérifiant les 2~con\-di\-tions initiales imposées est la fonction $h$ définie sur $\rset $ par $$ \dresultat {h (x) = {4\over 3} (x+1) e^{-2x}} $$ \partie {B} % \alphnum \ Comme $(1+x)' = 1$ et $\left( e^{-2x}\right) ' = -2e^{-2x}$, on vérifie facilement que $\dresultat { f' (x) = -{4\over 3} (2x+1)e^{-2x}. }$ \alph \ On a $f'$ sous forme d'un produit de facteurs. Or l'exponentielle est toujours strictement positive, $-4/3$ est toujours strictement négatif, et $(2x+1)$ est strictement positif pour $x$ positif. On en déduit que la dérivée $f' (x)$ est toujours négative quand $x\geq 0$, autrement dit que \tresultat {la fonction $f$ est décroissante sur $[0, +\infty [$}. \num \ On a \dresultat {\lim _{x\to +\infty } f (x) = 0} et donc une asymptote horizontale d'équation $y=0$, puisque $$ f (x) = {4\over 3} (1+x) e^{-2x} = {4\over 3} e^{-2x} + {4\over 3} x e^{-x} e^{-x} \qquad {\rm avec} \qquad \lim _{x\to +\infty } e^{-2x} = 0 = \lim _{x\to +\infty } xe^{-x} $$ \alphnum \ On sait que $$ e^t = 1 + t + {t^2 \over 2!} + {t^3 \over 3!} + t^3 \varepsilon (t) \qquad {\rm avec} \quad \lim _{t\to 0} \varepsilon (t) = 0. $$ d'où $$ e^{-2x} = 1 -2x + {(-2x)^2 \over 4} + {(-2x)^3 \over 6} + x^3 \varepsilon (x) \qquad {\rm avec} \quad \lim _{x\to 0} \varepsilon (x) = 0. $$ soit $$\dresultat { e^{-2x} = 1 -2x + 2x^2 - {4x^3 \over 3} + x^3 \varepsilon (x) \qquad {\rm avec} \quad \lim _{x\to 0} \varepsilon (x) = 0. }$$ \alph \ En multipliant cette dernière relation par ${4\over 3} (1+x)$, en ne prenant en compte que les termes d'ordre inférieur ou égal à 3, il vient alors $$\dresultat { f (x) = {4\over 3} \left( 1 - x + {2\over 3} x^3\right) + x^3 \varepsilon (x) \qquad {\rm avec} \quad \lim _{x\to 0} \varepsilon (x) = 0. }$$ \alph \ Cette relation nous donne immédiatement une équation de la tangente au point d'abscisse~0~: $$\dresultat { T~: y = {4\over 3} (1 - x) }$$ Quand à la position relative de $C$ et $T$ pour $x$ positif au voisinage de $0$, il suffit d'étudier le signe de la différence entre $f (x)$ et $T (x)$. Or ici on a $$ f (x) - T (x) = {4\over 9} x^3 + x^3 \varepsilon (x) \qquad {\rm avec} \quad \lim _{x\to 0} \varepsilon (x) = 0. $$ Comme ${4x^3\over 3}$ est positif pour $x$ positif, on en déduit que \tresultat {$C$ au dessus de $T$ pour $x$ positif au voisinage de $0$}. \alphnum \ On a $$ I = \int _0^3 f (x) \, dx = {4\over 3}\int _0^3 (1+x) e^{-2x} \, dx $$ Posons $$ U = 1+x \quad {\rm et} \quad V' = e^{-2x} \qquad \hbox {il vient alors} \qquad U' = 1 \quad {\rm et} \quad V = -{e^{-2x} \over 2} $$ D'où $$\eqalign { I &= {4\over 3} \left( - {1\over 2} \Big[ (1+x) e^{-2x}\Big] _0^3 + {1\over 2} \int _0^3 e^{-2x} \, dx \right) \cr &= {4\over 3} \left( - {1\over 2} \left( 4e^{-6} - 1\right) - {1\over 4} \Big[ e^{-2x} \Big] _0^3 \right) \cr &= {4\over 3} \left( - 2e^{-6} + {1\over 2} - {1\over 4} \left( e^{-6} - 1\right) \right) \qquad {\rm soit} \qquad \dresultat {I = 1 - 3e^{-6} \approx 0, 99} \cr }$$ Cette quantité représente, en unité d'aire, l'aire comprise entre la courbe $C$, l'axe $Ox$ et les droites verticales d'équation $x=0$ et $x=3$. \alph \ On a $$\displaylines { \lim _{t\to +\infty } \left( -{2\over 3} t - 1\right) e^{-2t} = \lim _{t\to +\infty } -{2\over 3} t e^{-t} e^{-t} + {2\over 3} e^{-2t} \qquad {\rm avec} \qquad \lim _{t\to +\infty } e^{-2t} = 0 = \lim _{t\to +\infty } te^{-t} \cr {\rm soit} \qquad \dresultat { \lim _{t\to +\infty } \left( -{2\over 3} t - 1\right) e^{-2t} = 0} \cr }$$ \alph \ Par définition de $A (t)$, on a $$ A (t) = \int _0^t f (x) \, dx \qquad {\rm soit} \qquad A (t) = \left( -{2\over 3} t - 1\right) e^{-2t} + 1. $$ En vertu des questions précédentes, on a donc bien évidemment \dresultat {J = 1} puisque $\displaystyle {J = \lim _{t\to +\infty } A (t)}$. \alph \ On a donc \dresultat {J-I = 3e^{-6} \approx 0, 07}, d'où \dresultat {0\leq J-I\leq 10^{-2}}. Et cette quantité représente l'aire du domaine plan infini compris entre la courbe $C$, l'axe $Ox$ et situé à droite de la droite verticale d'équation $x=3$. \fincorrige