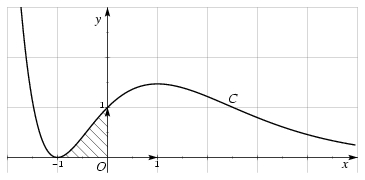
\exo {\' Equation différentielle, développement limité, relations fonctionnelles} \let \partie \centerpartie \centerline {\bf Les 3 parties de cet exercice peuvent être traitées de façon indépendante.} \partie {A -- Résolution d'une équation différentielle} On considère l'équation différentielle $$ y''- y' - 2y = (-6x-4) e^{-x} \leqno (E) $$ où $y$ est une fonction de la variable $x$, définie et deux fois dérivable sur $\rset $, $y'$ sa fonction dérivée première et $y''$ sa fonction dérivée seconde. \itemnum Résoudre sur $\rset $ l'équation différentielle $$ y'' - y' - 2y = 0 \leqno (E_0) $$ \itemnum Soit $h$ la fonction définie sur $\rset $ par~: \quad $h (x) = (x^2 + 2x) e^{-x}$. \item {} Démontrer que $h$ est une solution particulière de l'équation différentielle $(E)$. \itemnum En déduire l'ensemble des solutions de l'équation diférentielle $(E)$ \itemnum Déterminer la solution $f$ de l'équation différentielle $E$ qui vérifie les conditions initiales~: $$ f (0) = 1 \qquad {\rm et} \qquad f' (0) = 1. $$ \partie {B -- \' Etude d'une fonction} Soit $f$ la fonction définie sur $\rset $ par $f (x) = (x+1)^2 e^{-x}$. Sa courbe représentative $C$ dans un repère orthonormal est donnée sur la figure ci-après. \itemitemalphnum Calculer $\displaystyle { \lim _{x\to -\infty } f (x) }$. \itemitemalph Déterminer $\displaystyle { \lim _{x\to +\infty } x^2 e^{-x} }$ et $\displaystyle { \lim _{x\to +\infty } x e^{-x} }$. En déduire $\displaystyle { \lim _{x\to +\infty } f (x) }$. \itemitemalph Interpréter graphiquement le résultat obtenu au {\sl b\/}). \itemitemalphnum Démontrer que, pour tout $x$ de $\rset $, $f' (x) = (1-x^2) e^{-x}$. \itemitemalph Résoudre dans $\rset $ l'inéquation $f' (x) \geq 0$. \itemitemalph En déduire le sens de variation de $f$ sur $\rset $. \itemitemalphnum \` A l'aide du développement limité au voisinage de $0$ de la fonction exponentielle $t\mapsto e^t$, donner le développement limité, à l'ordre~$2$, au voisinage de $0$ de la fonction $x\mapsto e^{-x}$. \itemitemalph Démontrer que le développement limité, à l'ordre~$2$, au voisinage de~$0$ de la fonction $f$ est~: $$ f (x) = 1 + x - {1\over 2} x^2 + x^2 \varepsilon (x) = 0. $$ \itemitemalph En déduire une équation de la tangente $T$ à la courbe $C$ au point d'abscisse $0$ et la position relative de $C$ et $T$ au voisinage de ce point. \partie {C -- Calcul intégral} \itemitemalphnum La fonction $f$ définie dans la partie {\bf B} étant une solution de l'équation différentielle $(E)$~: $$ y'' - y' - 2y = (-6x-4) e^{-x}, $$ montrer que $f$ vérifie, pour tout $x$ de $\rset $, $$ f (x) = {1\over 2} \left[ f'' (x) - f' (x) + (6x+4) e^{-x}\right]. $$ \itemitemalph Soit $F$ la fonction définie sur $\rset $ par~: $$ F (x) = {1\over 2} \left[ f' (x) - f (x) - (6x+10) e^{-x}\right]. $$ Montrer que $F$ est une primitive de $f$. \itemalph Vérifier que, pour tout $x$ de $\rset $, $$ F (x) = (-x^2 -4x-5) e^{-x}. $$ \itemnum Utiliser ce qui précède pour démontrer que l'aire $A$ de la partie du plan hachurée sur la figure est, en unité d'aire, $$ A = e - 5. $$ \def \epspath{% $DATABASE/btsmai/analyse/equadiff/} $$ \epsillustrate {equ2_025.ps} $$ \finexo \corrige \let \partie \llappartie \partie {A} \vskip -5mm \itemnum L'équation caractéristique associée à l'équation $(E_0)$ est $r^2 - r - 2 = 0$, de discriminant $\Delta = 9$ et admettant les deux racines réelles distinctes $r_1 = -1$ et $r_2 = 2$. On en déduit que la solution générale de $E_0$ est~: $$ \tresultat { $y_0 (x) = Ae^{-x} + Be^{2x}$ où $A$ et $B$ constantes réelles quelconques}. $$ \itemnum On a $$ h (x) = (x^2 + 2x)e^{-x}, \qquad \qquad h' (x) = (-x^2 + 2)e^{-x}, \qquad \qquad h'' (x) = (x^2 - 2x - 2)e^{-x}. $$ d'où $$ h'' - h' - 2h = (-6x - 4) e^{-x}, $$ ce qui prouve que \tresultat {$h$ est une solution particulière de $(E)$}. \itemnum On en déduit que la solution générale de $(E)$ est $y = y_0 + h$, soit $$ \tresultat { $y (x) = (x^2 + 2x + A) e^{-x} + Be^{2x}$ où $A$ et $B$ constantes réelles quelconques}. $$ \itemnum Si $f (x) = (x^2 + 2x + A) e^{-x} + Be^{2x}$, alors $f' (x) = (-x^2 - A +2) e^{-x} + 2Be^{2x}$. Les deux conditions initiales nous fournissent alors le système $$ \matrix { \scriptstyle (1) \cr \scriptstyle (2) \cr } \cases { f (0) = A+B = 1 \cr f' (0) = 2B + 2 - A = 1 \cr } \qquad \Longrightarrow \qquad \matrix { \scriptstyle (1) \cr \scriptstyle (1) + (2) \cr } \cases { A+B = 1 \cr 3B + 2 = 2 \cr } \qquad \Longrightarrow \qquad (A, B) = (1, 0). $$ D'où la solution particulière $f$ cherchée~: \dresultat {f (x) = (x^2 + 2x + 1) e^{-x} = (x+1)^2 e^{-x}}. \partie {B} \vskip -5mm \itemalphnum Il vient $$ \lim _{x\to -\infty } f (x) = \lim _{x\to -\infty } x^2 \left( 1 + {2\over x} + {1\over x^2}\right) e^{-x} \qquad {\rm or} \qquad \cases { \lim _{-\infty } x^2 = +\infty \cr \lim _{-\infty } 1 + 2/x + 1/x^2 = 1 \cr \lim _{-\infty } e^{-x} = +\infty \cr } $$ d'où \dresultat {\lim _{x\to -\infty } f (x) = +\infty }. (on aurait également pu utiliser les équivalents en l'infini.) \itemalph On a \dresultat { \lim _{x\to +\infty } x^2 e^{-x} = 0 = \lim _{x\to +\infty } x e^{-x} } d'après le cours. Or $f (x) = x^2 e^{-x} + 2xe^{-x} + e^{-x}$. On en déduit donc que \dresultat {\lim _{x\to +\infty } f (x) = 0} puisque $\displaystyle { \lim _{x\to +\infty } e^{-x} = 0 }$. \itemalph Graphiquement, ce dernier point signifie que \tresultat {l'axe $Ox$ est une asymptote horizontale en $+\infty $ pour la courbe $C$}. \itemalphnum Vu au \boxit {2pt}{\bf A}~{\bf 4.} en prenant $A=1$, on trouve bien \dresultat {f' (x) = (1-x^2) e^{-x}}. \itemalph \alph \ L'expression $e^{-x}$ est toujours strictement positive, donc $f' (x)$ est du signe de $1-x^2$, polynôme du second degré qui se factorise en $(1-x) (1+x)$. Il admet donc les deux racines réelles $-1$et $1$ et il est positif entre ces racines (signe de $-a$). D'où la tableau récapitulatif suivant~: $$\dresultat { \vcenter {\offinterlineskip \eightpoint \rm \def \cc#1{ \hfil #1 \hfil } \halign { % preamble \cc {$#$}& #\tv && \cc {$#$} \cr x&& -\infty && -1&& 1&& +\infty \cr \noalign {\hrule height 1pt} f' (x)&& &-& 0&+& 0& -& \cr \noalign {\hrule height 1pt} \buucenter {$f (x)$}&& \buup {$+\infty $}& \brightddownarrow & \down {0}& \brightuuparrow & \buup {$4/e$}& \brightddownarrow & \down{$0$} \cr }} }$$ \itemalphnum On sait que $$ e^t = 1 + t + {t^2\over 2} + t^2 \varepsilon (t) \quad {\rm avec} \quad \lim _{t\to 0} \varepsilon (t) = 0 \qquad {\rm d'où} \qquad \dresultat { e^{-x} = 1 - x + {x^2\over 2} + x^2 \varepsilon (x) \quad {\rm avec} \quad \lim _{x\to 0} \varepsilon (x) = 0 } $$ \itemalph Il vient $$\eqalign { (1+2x+x^2) e^{-x} &= \big( 1+2x+x^2 \big) \left( 1 - x + {x^2\over 2}\right) + x^2 \varepsilon (x) \quad {\rm avec} \quad \lim _{x\to 0} \varepsilon (x) = 0 \cr &= \left( 1+2x+x^2 - x -2x^2 + {x^2\over 2}\right) + x^2 \varepsilon (x) \quad {\rm avec} \quad \lim _{x\to 0} \varepsilon (x) = 0 \cr } $$ soit $$\dresultat { f (x) = 1 + x - {1\over 2} x^2 + x^2 \varepsilon (x) \quad {\rm avec} \quad \lim _{x\to 0} \varepsilon (x) = 0 }$$ \itemalph Pour avoir l'équation de la tangente en $0$, il suffit de regarder le développement limité d'ordre~$1$, d'où l'équation cherchée \dresultat {T~: y = 1+x}. Quand à la position relative, elle est donnée par le signe de la différence entre $f (x)$ et $1+x$. Au voisinage de $0$, cette différence est égale à $- {1\over 2} x^2 + x^2 \varepsilon (x)$, et elle est toujours négative (puisque $x^2$ positif) pour peu que $x$ soit suffisamment proche de $0$. On en conclut que, localement, \tresultat {$T$ est au dessus de $C$ au voisinage de $0$}. \partie {C} \vskip -5mm \itemalphnum La fonction $f$ étant solution de l'équation $(E)$, elle vérifie la relation $$\displaylines { f'' (x) - f' (x) - 2f (x) = (-6x-4) e^{-x} \qquad {\rm d'où} \qquad 2f (x) = f'' (x) - f' (x) + (6x+4) e^{-x} \cr {\rm et\ donc} \qquad \dresultat { f (x) = {1\over 2} \left[ f'' (x) - f' (x) + (6x+4) e^{-x}\right] } }$$ \itemalph On a $$ F (x) = {1\over 2} \left[ f' (x) - f (x) - (6x+10) e^{-x}\right] \qquad {\rm d'où} \qquad F' (x) = {1\over 2} \underbrace {\left[ f'' (x) - f' (x) - (-6x-4) e^{-x}\right] } _{\hbox {$= 2 f (x)$ d'après {\sl a\/})}} $$ et on a bien \dresultat {F' (x) = f (x)}. On a $$ f (x) = (x^2 + 2x + 1) e^{-x} \qquad {\rm et} \qquad f' (x) = (1 - x^2) e^{-x} $$ Il vient alors $$\eqalign { F (x) &= {1\over 2} \left[ f' (x) - f (x) - (6x+10) e^{-x}\right] \cr &= {1\over 2} \left( 1-x^2 - x^2 - 2x - 1 - (6x+10)\right) e^{-x} \cr &= {1\over 2} (-2x^2 - 8x - 10) e^{-x} \qquad {\rm soit} \qquad \dresultat {F (x) = (-x^2 -4x -5) e^{-x}}. \cr }$$ \itemnum On a $$ A = \int _{-1}^0 f (x) \, dx = \Big[ F (x)\Big] _{-1}^0 = F (0) - F (-1) \qquad {\rm soit} \qquad \dresultat {A = -5 + 2e}. $$ \fincorrige