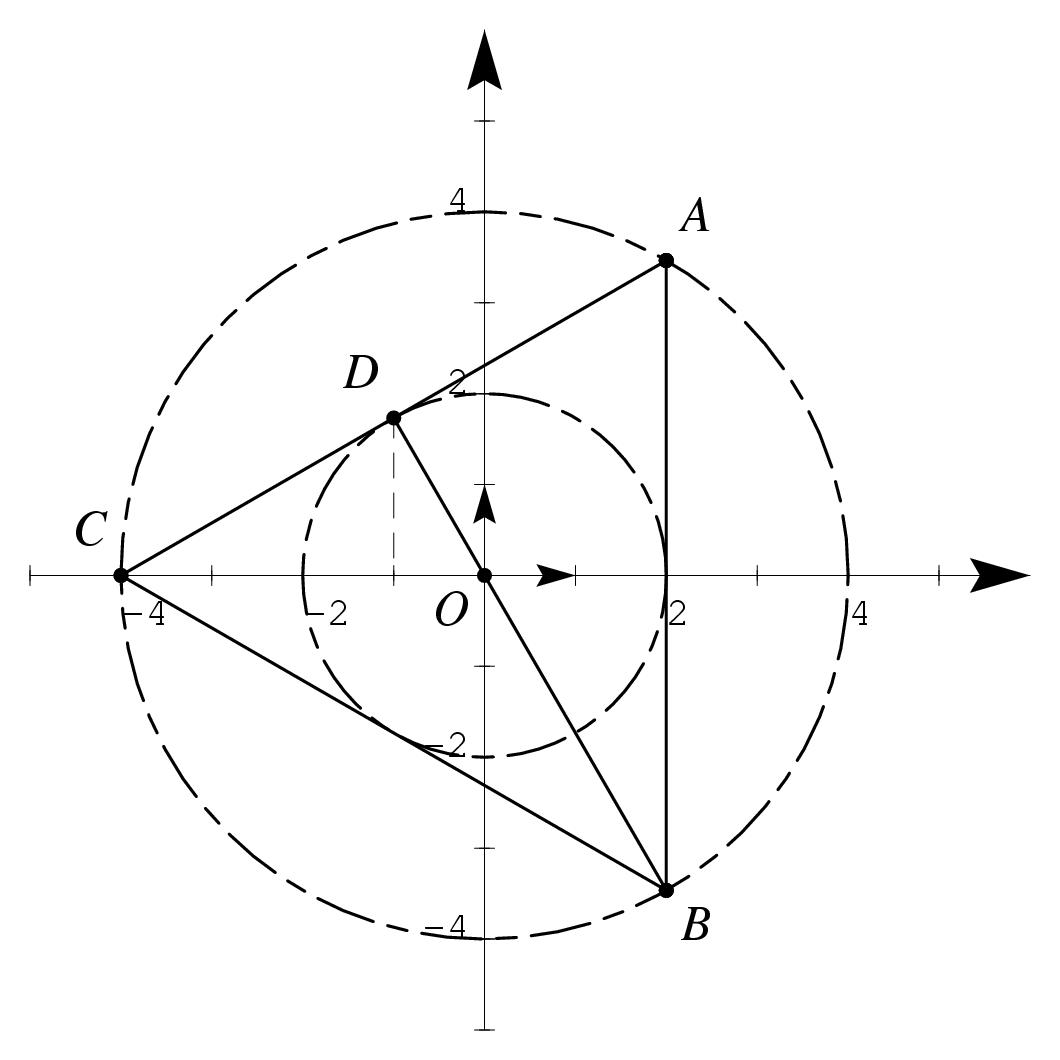
\exo{Complexes et géométrie} Le plan complexe est muni d'un repère orthonormal $(O, \vec u, \vec v)$ d'unité graphique 1~cm (ou 1~grand carreau si vous préférez). \itemnum On considère les deux nombres complexes $$ z_A = \left[ 4, {\pi \over 3} \right] \qquad {\rm et} \qquad z_B = 2 - 2i \sqrt 3. $$ \itemitemalph Déterminer la forme algébrique du nombre $z_A$. \itemitemalph Déterminer la forme trigonométrique du nombre $z_B$. \itemitemalph Placer dans le plan les points $A$ et $B$ d'affixes respectives $z_A$ et $z_B$. (On laissera des traces des constructions.) \itemnum On considère les deux nombres complexes $$ z_C = -4 \qquad {\rm et} \qquad z_D = -1 + i \sqrt 3. $$ \itemitemalph Calculer le module et un argument de chacun de ces deux nombres complexes. \itemitemalph Placer dans le plan complexe les points $C$ et $D$ d'affixes respectives $z_C$ et $z_D$. \itemitemalphnum Démontrer que les points $A$, $B$ et $C$ appartiennent à un même cercle de centre~$O$. \itemitemalph Démontrer que $D$ est le milieu du segment $[AC]$. \itemitemalph Démontrer que le triangle $BDA$ est rectangle. \itemitemalph Démontrer que le triangle $ABC$ est équilatéral. \finexo \corrige{} \itemalphnum Par définition, on a $$ a = 4 \left( \cos \left( {\pi \over 3}\right) + i \sin \left( {\pi \over 3}\right) \right) = 4 \left( {1\over 2} + i {\sqrt3 \over 2}\right) \qquad {\rm soit} \qquad \mresultat{a = 2 + 2i \sqrt 3} $$ \itemalph Le module de $z_B$ est $|z_B| = \sqrt {2^2 + (-2\sqrt 3)^2} = \sqrt {4 + 12}$, soit \mresultat{|z_B| = 4}. Son argument $\theta_B$ vérifie les relations $$ \cases{ \cos \theta_B = {2 \over 4} \cr \sin \theta_B = - {2\sqrt 3 \over 4} \cr} \qquad {\rm soit} \qquad \cases{ \cos \theta_B = {1 \over 2} \cr \sin \theta_B = -{\sqrt 3 \over 2} \cr} \qquad \hbox{d'où l'on tire} \qquad \dresultat{\theta_B = -{\pi \over 3 }} \quad \hbox{à $2k\pi $ près} $$ On a donc finalement \dresultat{z_B = \left[ 4, -{\pi \over 3} \right]} \itemalph \def \epspath{% $HOME/tex_doc/lycee/database//1ere/sti/algebre/complex/} \epsfxsize = 80mm $$ \superboxepsillustrate{geom_005.ps} $$ \itemalphnum De la même manière que précedemment, on trouve \mresultat{|z_C| = 4} et $\cos \theta_C = -1$ avec $\sin \theta_C = 0$. On en déduit que \mresultat{\theta_C = \pi } convient. \item{} Pour $z_D$, on trouve \mresultat{|z_D| = 2} d'où $\cos \theta_D = -1/2$ et $\sin \theta_D = {\sqrt 3 \over 2}$. On en déduit que \mresultat{\theta_D = 2\pi /3} à $2k\pi $ près. Finalement, on a $$ \dresultat{z_C = [4, \pi]} \qquad {\rm et} \qquad \dresultat{z_D = \left[ 2, {2\pi \over 3} \right]} $$ \itemalphnum On a $|z_A| = |z_B| = |z_C| = 4$, donc on a l'égalité de distances $OA = OB = OC = 4$. En d'autres termes, les points $A$, $B$ et $C$ sont tous sur le \tresultat{même cercle de centre $O$ et de rayon 4}. \itemalph Le milieu du segment $[AC]$ a pour affixe $$ {1 \over 2} (z_A + z_C) = {1 \over 2} (2 + 2i\sqrt 3 - 4) = -1 + i \sqrt 3 = z_D $$ Donc \tresultat{$D$ est bien le milieu de $[AC]$}. \itemalph On calcule les différentes distances concernées, puis on applique le théorème de Pythagore~: $$\displaylines{ AB = |z_B - z_A| = |(2-2i\sqrt 3) - (2+2i\sqrt 3)| = |-4i\sqrt3| = \sqrt {48} \qquad {\rm soit} \qquad \mresultat{AB = 4\sqrt 3} \cr AD = |z_D - z_A| = |(-1+i\sqrt 3) - (2+2i\sqrt 3)| = |-3 -i\sqrt 3| = \sqrt {12} \qquad {\rm soit} \qquad \mresultat{AD = 2\sqrt 3} \cr BD = |z_D - z_B| = |(-1+i\sqrt 3) - (2-2i\sqrt 3)| = |-3 + 3i\sqrt 3| = \sqrt {36} \qquad {\rm soit} \qquad \mresultat{BD = 6} \cr }$$ On a bien $AB^2 = AD^2 + BD^2$ donc \tresultat{$BDA$ rectangle en $D$}. \itemalph Il suffit de calculer les deux distances encore inconnues~: $$\displaylines{ AC = |z_C - z_A| = |-4 - (2+2i\sqrt 3)| = |-6 -2i\sqrt 3| = \sqrt {48} \qquad {\rm soit} \qquad \mresultat{AC = 4\sqrt 3} \cr BC = |z_C - z_B| = |-4 - (2-2i\sqrt 3)| = |-6 +2i\sqrt 3| = \sqrt {48} \qquad {\rm soit} \qquad \mresultat{BC = 4\sqrt 3} \cr }$$ Finalement, on a $AC = BC = AB$ donc \tresultat{$ABC$ est équilatéral}. \fincorrige