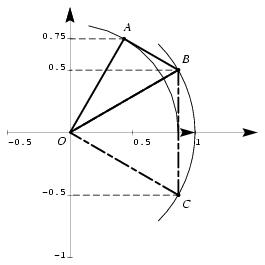
\exo {Triangle rectangle et triangle équilatéral} Le plan complexe est rapporté au repère orthonormal $(O, \vec u, \vec v)$. On désigne par $i$ le nombre complexe de module~1 et d'argument $\pi /2$. On considère les trois nombres complexes $$ a = {\sqrt 3\over 4} (1 + i\sqrt 3), \qquad \qquad b = \left[ 1, {\pi \over 6}\right], \qquad {\rm et} \qquad c = \overline b $$ où $\overline b$ désigne le conjugué du nombre complexe $b$. \itemnum Déterminer la forme algébrique des nombres $b$ et $c$. (Autrement dit, écrire $b$ et $c$ sous la forme $x+iy$ avec $x$ et $y$ réels.) \itemnum Déterminer le module de chacun des 4~nombres $$ a, \qquad c, \qquad b-c, \qquad a-b. $$ \itemnum On désigne par $A$, $B$ et $C$ les points du plan complexe d'affixes respectives $a$, $b$ et $c$. \itemitemalph Placer les points $A$, $B$ et $C$ dans le repère orthonormal $(O, \vec u, \vec v)$ (on demande une construction exacte pour $B$ et $C$, et une construction approchée pour le point $A$). \itemitemalph Démontrer que le triangle $OBC$ est équilatéral. \itemitemalph Démontrer que le triangle $0AB$ est rectangle. \finexo \corrige \catcode`\|=12 \everymath = {\displaystyle } \itemnum On a $b = \cos \left( {\pi \over 6}\right) + i \sin \left( {\pi \over 6}\right) $, soit \dresultat {b = {\sqrt 3\over 2} + {1\over 2}i}. D'où \dresultat {c = {\sqrt 3\over 2} - {1\over 2}i}. \itemnum On a $$\displaylines { |a| = \left \vert {\sqrt 3\over 4} \right \vert \times |1 + i\sqrt 3| = \sqrt {3\over 16} \times \sqrt {1+3} = {\sqrt 3\over 4} \times 2 \qquad {\rm soit} \qquad \dresultat {|a| = {\sqrt 3\over 2}} \cr |c| = \sqrt {{3\over 4} + {1\over 4}} \qquad {\rm soit} \qquad \dresultat {|c| = 1} \cr |b-c| = \left \vert {\sqrt 3\over 2} + {1\over 2}i - {\sqrt 3\over 2} + {1\over 2}i\right \vert = |i| \qquad {\rm soit} \qquad \dresultat {|b-c| = 1} \cr |a-b| = \left \vert {\sqrt 3 \over 4} + {3\over 4}i - {\sqrt 3\over 2} - {1\over 2}i\right \vert = \left \vert -{\sqrt 3 \over 4} + {1\over 4}i\right \vert = \sqrt {{3\over 16} + {1\over 16}} \qquad {\rm soit} \qquad \dresultat {|a-b| = {1\over 2}} \cr }$$ \def \epspath {% $HOME/tex_doc/lycee/database/1ere/sti/algebre/complex/} \epsfxsize = 80 mm \itemalphnum $$ \superboxepsillustrate {geom_006.ps} $$ \itemalph On a $CB = |b-c| = 1$, $OB = |b| = 1$ et $OC = |c| = 1$, donc \tresultat {$OBC$ est équilatéral} \itemalph On a $OA = |a| = \sqrt 3/2$, $OB = |b| = 1$ et $BA = |a-b| = 1/2$. On vérifie que l'on a bien $OA^2 + BA^2 = OB^2$ et on en déduit, par Pythagore, que \tresultat {$OAB$ rectangle en $A$} \fincorrige