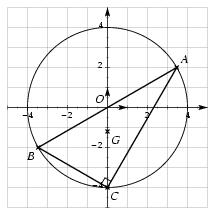
\exo {Complexes et géométrie} \itemnum On considère le nombre complexe $z_1$ défini par $$ z_1 = \Big[ 4 ; -{5\pi \over 6}\Big]. $$ Déterminer la forme algébrique de $z_1$. \itemnum On considère les nombres complexes $z_A$, $z_B$ et $z_C$ définis par $$ z_A = 2\sqrt 3 + 2i \qquad \qquad z_B = -2\sqrt 3 -2i \qquad \qquad z_C = -4i. $$ \itemitemalph Déterminer le module et un un argument de $z_A$. \itemitemalph Déterminer le module de $z_B$. \itemitemalph Déterminer le module et un un argument de $z_C$. \itemnum Dans le plan rapporté à un repère orthonormal $(O, \vec u, \vec v)$ d'unité graphique $2$~cm (ou $2$~grands carreaux), placer les points $A$, $B$ et $C$ d'affixes respectives $z_A$, $z_B$, $z_C$. \itemnum Montrer que les points $A$, $B$ et $C$ sont situés sur un même cercle de centre $O$ dont on précisera le rayon. \itemitemalphnum Calculer la distance $AB$. \itemitemalph Montrer que le triangle $ABC$ est un triangle rectangle. \itemnum Soit $G$ le centre de gravité du $ABC$. Déterminer l'affixe $z_G$ du point $G$. \finexo \corrige \itemnum Il vient $$ z_1 = 4 \Big( \cos {-5\pi \over 6} + i \sin {-5\pi \over 6}\Big) = 4 \Big( -{\sqrt 3\over 2} - {1 \over 2}i\Big) \qquad {\rm soit} \qquad \dresultat {z_1 = -2\sqrt 3 - 2i} $$ \itemalphnum Il vient $$ |z_A| = \sqrt {(2\sqrt 3)^2 + 2^2} = 4 \qquad {\rm et} \qquad \cases { \cos \theta _A = 2\sqrt 3 /4 = \sqrt 3 /2 \cr \sin \theta _A = 1/2 \cr } \quad \Longrightarrow \quad \theta _A = {5\pi \over 6} \quad \rm convient $$ d'où \dresultat {z_A = \Big[ 4 ; {5\pi \over 6}\Big]} \itemalph Il vient $$ |z_B| = \sqrt {(-2\sqrt 3)^2 + (-2)^2} = \dresultat {4 = |z_B|} $$ \itemalph Il vient $$ |z_C| = \sqrt {(-4)^2} = 4 \qquad {\rm et} \qquad \cases { \cos \theta _C = 0 \cr \sin \theta _C = -1 \cr } \quad \Longrightarrow \quad \theta _C = -{\pi \over 2} \quad \rm convient \qquad et \qquad \dresultat {z_C = \Big[ 4 ; -{\pi \over 2}\Big]} $$ \itemnum \def \epspath {% $HOME/tex_doc/lycee/database/1ere/sti/algebre/complex/} $$ \superboxepsillustrate {geom_009.ps} $$ \itemnum On sait, d'après les questions précédentes, que $$ |z_A| = 4, \qquad \qquad |z_B| = 4, \qquad {\rm et} \qquad |z_C| = 4, \qquad \hbox {autrement dit}, \qquad OA = OB = OC = 4 $$ ce qui prouve que les points $A$, $B$ et $C$ sont \tresultat {sur un même cercle de centre $O$ et de rayon $4$}. \catcode`\|=12 \itemalphnum Il vient $$\eqalign { AB &= |z_B - z_A| \cr &= \left| -2\sqrt 3 - 2i - \big(2\sqrt 3 + 2i\big) \right| \cr &= \left| -4\sqrt 3 - 4i\right| \cr &= \sqrt { (-4\sqrt 3)^2 + (- 4)^2} \qquad {\rm soit} \qquad \dresultat {AB = 8}. \cr }$$ \itemalph Les points $A$, $B$ et $C$ sont tous sur le même cercle de centre $O$ et de rayon $4$ d'après la question {\bf 3.}, et $AB = 8$ d'après la question précédente. On en déduit que $[AB]$ est un diamètre du cercle, ce qui prouve que \tresultat {$ABC$ est un triangle rectangle en $C$}. \itemnum Si $G$ est le centre de gravité du triangle $ABC$, il vérifie l'égalité $$ \overrightarrow {OG} = {1\over 3} \overrightarrow {OC} $$ puisque $O$ est le milieu de $[AB]$ (car centre du cercle dont $[AB]$ est un diamètre). De cette égalité vectorielle, on tire l'égalité d'affixes~: $$ z_G = {1\over 3} z_C = {1\over 3} \times (-4i) \qquad {\rm soit} \qquad \dresultat {z_G = - {4\over 3}i}. $$ \fincorrige