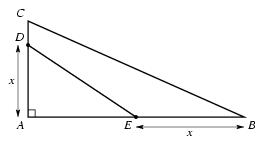
\exo {Triangles rectangles\dots } On considère un triangle $ABC$ rectangle en $A$ tel que $AB = 18$ et $AC = 8$. On place les points $D$ et $E$ respectivement sur $[AC]$ et $[AB]$, avec $AD = BE = x$. Le but de cet exercice est de déterminer $x$ pour que l'aire du triangle $ADE$ soit égale à la moitié de celle du triangle $ABC$. \itemitemalphnum Faire une figure. \itemitemalph Montrer que résoudre le problème posé revient à résoudre dans $[0; +\infty [$ l'équation~: $$ - {1\over 2} x^2 + 9x - 36 = 0. \leqno (E) $$ \itemnum Répondre au problème posé. \finexo \corrige {} \def \epspath {% $HOME/tex_doc/lycee/database/1ere/sti/algebre/polynome/} %\epsfxsize = 80mm $$ \superboxepsillustrate {geom_004.ps} $$ \itemnum L'aire du triangle $ABC$ est ${1\over 2} (AB \times AC) = {1\over 2} (18 \times 8)$, soit \dresultat {{\cal A}_{ABC} = 72}. \item {} L'aire du triangle $ADE$ est ${1\over 2} (AD \times AE) = {1\over 2} (x \times (18-x))$, soit \dresultat {{\cal A}_{ADE} = - {1\over 2} x^2 + 9x}. \item {} Répondre au problème posé revient donc à résoudre l'équation $$ {\cal A}_{ADE} = {1\over 2} {\cal A}_{ABC} \qquad \Longleftrightarrow \qquad - {1\over 2} x^2 + 9x = 36 \qquad \Longleftrightarrow \qquad \dresultat {- {1\over 2} x^2 + 9x - 36 = 0}. $$ \itemnum On a maintenant une équation polynomiale du type $ax^2 + bx + c = 0$ avec $$ a = - {1\over 2}, \qquad b = 9, \qquad c = - 36. $$ Le calcul du discriminant $\Delta $ donne \dresultat {\Delta = {9}} d'où l'on déduit que l'équation admet 2~solutions~: $x = 6$ et $x = 12$. Or on sait que $x \leq AC = 8$, donc la solution $x = 12$ est impossible. \item {} Finalement, le problème posé admet \tresultat {une seule solution~: $x = 6$}. \fincorrige