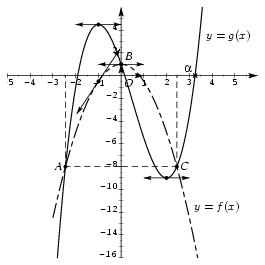
\exo {\'Etudes de fonctions polynômes, résolution approchée d'équation} \let \partie \centerpartie Le plan est rapporté à un repère orthogonal $(O, \vec \imath, \vec \jmath \,)$ d'unité $2~\cm $ sur $Ox$ et $1~\cm $ sur $Oy$. \partie {A -- \' Etude d'une fonction polynôme de degré 2} On note $C_f$ la courbe représentative de la fonction $f$ définie sur $[-3, 4]$ par $$ f (x) = -{3\over2} x^2 + 1. $$ \itemitemalphnum Déterminer $f'$, la fonction dérivée de $f$. \itemitemalph \'Etudier le signe de $f' (x)$ pour $x\in [-3; 4]$. \itemitemalph En déduire le tableau de variation de $f$ sur $[-3; 4]$. \itemnum Déterminer une équation de $T$, la tangente à la courbe $C_f$ au point d'abscisse $-1$. \itemnum Tracer la tangente $T$ puis la courbe $C_f$ dans le repère $(O, \vec \imath, \vec \jmath \,)$. \partie {B -- \' Etude d'une fonction polynôme de degré 3} On considère $C_g$, la courbe représentative de la fonction $g$ définie sur $[-3, 4]$ par $$ g (x) = x^3 - {3\over2} x^2 - 6x + 1. $$ \itemitemalphnum Déterminer la fonction dérivée $g'$. \itemitemalph Expliquer pourquoi $g' (x)$ est du signe de $x^2 - x -2$. \itemitemalph \'Etudier le signe de $g' (x)$. En déduire le tableau de variation de $g$ sur $[-3, 4]$. \itemitemalphnum Combien l'équation $g (x) = 0$ admet-elle de solution(s) sur $[-3, 4]$~? (Justifier.) On note $\alpha$ la plus grande de ces solutions. \itemitemalph Déterminer un encadrement d'amplitude $10^{-2}$ de $\alpha$ (justifier). \itemnum Déterminer, par le calcul, les coordonnées des points d'intersection des courbes $C_f$ et $C_g$. \itemnum Déterminer les positions relatives des courbes $C_f$ et $C_g$. On récapitulera les résutats dans un tableau. \itemnum Tracer la courbe $C_g$ dans le repère orthogonal $(O, \vec \imath, \vec \jmath\,)$. \finexo \corrige{} \let \partie \llappartie \partie {A} \vskip -5mm \itemnum Il vient \mresultat {f' (x) = -3x}, du signe de $-x$, d'où le tableau de variations~: $$\dresultat{ \vbox{\eightpoint\rm \def \hfq{\hfil \hskip .3em } \offinterlineskip \halign{ % preamble &\cc{$#$} \cr x& \vrule depth 5pt & -3&& 0&& 4% \cr \noalign{\hrule} f' (x)& \vrule height 10pt depth 5pt & & + &0& - \cr \noalign{\hrule} \bbuucenter{$f (x)$}& \vrule& \down{$-12, 5$}& \bbrightuuparrow & \bbuup{$1$}& \bbrightddownarrow & \down{$-23$} \cr }} }$$ \itemnum On a $f (-1) = -1/2$ et $f' (-1) = 3$. L'utilisation de la formule $y = f' (a) (x-a) + f (a)$ donne alors $$ y = 3 (x+1) - {1\over 2} \qquad \hbox {d' où l'équation cherchée~:} \qquad \dresultat {T~: \quad y = 3x + {5\over 2}} $$ \itemnum \def \epspath{% $HOME/tex_doc/lycee/database/1ere/sti/analyse/etudes/} %$ \epsfxsize = 80mm $$ \superboxepsillustrate{pol_001.ps} $$ \partie {B} \vskip -7mm \itemalphnum \alph \ Le calcul de la fonction dérivée donne \dresultat {g' (x) = 3x^2 - 3x - 6}, qui est bien \tresultat {du signe de $x^2 - x -2$} puisque $g' (x) = 3 (x^2 - x - 2)$ avec $3$ positif. \itemalph La méthode du discriminant $\Delta$, ici égal à 9, nous donne les deux racines $x_1 = 2$ et $x_2 = -1$. Or l'on sait qu'un polynôme du second degré est \og {\sl du signe de $-a$ entre les racines}\fg. D'où~: \tresultat {$g'$ négatif entre $-1$ et $2$, positif sinon}. D'où le tableau de variations de $g$~: $$\dresultat{ \vbox{\eightpoint\rm \def \hfq{\hfil \ } \offinterlineskip \halign{ % preamble &\cc{$#$} \cr x& \vrule depth 5pt & -3&& -1&& 2&& 4&% \cr \noalign{\hrule} g' (x)& \vrule height 10pt depth 5pt & & + &0& - &0& + & \cr \noalign{\hrule} \bbuucenter{$g (x)$}& \vrule& \down{$-21, 5$}& \bbrightuuparrow & \bbuup{$9/2$}& \bbrightddownarrow & \down{$-9$} & \bbrightuuparrow & \bbuup{$17$}& \cr }} }$$ \itemalph La fonction $g$ est strictement croissante sur l'intervalle $[-3, 1]$ (d'après le tableau de va\-ria\-tions) et elle change de signe sur cet intervalle (puisque $g (-3) = -21, 5 < 0$ et $g (-1) = 4, 5 > 0$). Donc l'équation $g (x) = 0$ admet une unique solution sur l'intervalle $[-3, -1]$. \item {} On tient des raisonnements analogues pour mon\-trer que cette équation admet également une u\-ni\-que solution sur l'intervalle $[-1, 2]$ ainsi qu'une unique solution sur l'intervalle $[2, 4]$. Finalement, l'équation $g (x) = 0$ admet $$ \tresultat{3 solutions sur l'intervalle $[-3, 4]$}. $$ \itemalph On a \mresultat{3, 25 < \alpha < 3, 26} puisque $g (3, 25) \approx -0, 016$ est négatif, alors que $g (3, 26) \approx 0, 145$ est positif. \itemalph Pour déterminer l'intersection des deux courbes, il faut résoudre le système $$\displaylines{ \cases{ y = g (x) \cr y = f (x) \cr} \quad \Longleftrightarrow \quad \cases{ y = x^3 - {3\over2} x^2 - 6x + 1 \cr y = -{3\over2} x^2 + 1 \cr} \quad \Longleftrightarrow \quad \cases{ -{3\over2} x^2 + 1 = x^3 - {3\over2} x^2 - 6x + 1 \cr y = -{3\over2} x^2 + 1 \cr} \cr \Longleftrightarrow \quad \cases{ 0 = x^3 - 6x \cr y = -{3\over2} x^2 + 1 \cr} \quad \Longleftrightarrow \quad \cases{ 0 = x (x - \sqrt6) (x+\sqrt6) \cr y = -{3\over2} x^2 + 1 \cr} }$$ d'où les trois points d'intersection~: \mresultat{A (-\sqrt6, -8)}, \mresultat{B (0, 1)} et \mresultat{C (\sqrt6, -8)}. \itemnum Pour étudier les positions relatives des courbes $C_f$ et $C_g$, il faut étudier le signe de $f (x) - g (x)$. Il vient~: $$\eqalign { f (x) - g (x) &= \left( -{3\over2} x^2 + 1\right) - \left( x^3 - {3\over2} x^2 - 6x + 1\right) \cr &= -x^3 + 6 x = \dresultat {x (6-x^2) = f(x) - g(x)} }$$ Comme $6-x^2$ a les deux racines évidentes $\sqrt 6$ et $-\sqrt 6$, et que ce polynôme est positif entre les racines (signe de $-a$), on a le tableau de signes et le récapitulatif~: \medskip \centerline { $$\dresultat { \vcenter {\offinterlineskip \eightpoint \rm \halign { % preamble \cc {$#$}& #\tv width 1pt & $#$ & \cc {$#$}& \cc {$#$}& \cc {$#$}& \cc {$#$}& \cc {$#$}& \cc {$#$}& \cc {$#$}& $#$ \cr x&& -3 && -\sqrt 6 && 0&& \sqrt 6&& 4 \cr \noalign {\hrule height 1pt } x && & - &\tv & -& 0& + & \tv & +& \cr \noalign {\hrule } 6-x^2 && & - & 0& + &\tv & +& 0& -& \cr \noalign {\hrule height 1pt } f (x) - g (x) && & + & 0 & - &0& + &0 &- \cr \noalign {\hrule height 1pt } \hbox {positions relatives}& \tvi height 15pt& & \matrix {C_f {\rm \ au}\cr {\rm dessus\ de\ } C_g }& \tv & \matrix {C_f {\rm \ au}\cr {\rm dessous\ de\ } C_g }& \tv & \matrix {C_f {\rm \ au}\cr {\rm dessus\ de\ } C_g }& \tv & \matrix {C_f {\rm \ au}\cr {\rm dessous\ de\ } C_g }& \cr }}} $$ } \medskip \fincorrige \endinput \def \epspath{% $HOME/tex_doc/lycee/database/1ere/sti/analyse/etudes/} % \epsfxsize = 80mm % \rightsuperboxepsillustrate{pol_001.ps}{-22} \fincorrige