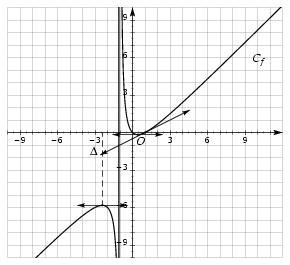
\exo{Une fonction rationnelle} On considère la fonction $f$ définie sur l'intervalle $]+\infty , -1[ \; \cup \; ]-1, +\infty[$ par $$ f (x) = {2 \over x + 1} + x - 2 $$ et on désigne par $C_f$ sa courbe représentative. \itemitemalphnum Calculer la fonction dérivée $f'$, et montrer que $$ f' (x) = {x^2 + 2x - 1 \over (x+1)^2} $$ \itemitemalph \'Etudier le signe de $f'$. En déduire le tableau de variations de $f$. \itemnum Déterminer une équation de $\Delta$, la tangente à la courbe $C_f$ au point d'abscisse $1$ %% \itemnum Montrer que la courbe $C_f$ admet une tangente parallèle à %% $\Delta $. Préciser en quel point. \itemnum \`A l'aide d'une calculatrice, remplir le tableau suivant en calculant, pour chaque valeur donnée de $x$, une valeur approchée à $10^{-2}$ près de $f (x)$. $$ \vbox{\halign{ % preamble \tv #&& \cc{$#$}& \tv # \cr \noalign{\hrule} & x&& -{9\over10}&& -{4\over5}&& -{3\over4}&& -{1\over2} && 0&& 1&& 2&& 3&& 4&& 9&& 15& \cr \noalign{\hrule} & f (x)&& && && && && && && && && && && & \cr \noalign{\hrule} }} $$ \itemnum Tracer soigneusement, dans un même repère orthogonal, la droite $\Delta$ et la courbe $C_f$. \finexo \corrige{} \itemnum On remarque tout d'abord que $f (x)$ existe si et seulement si \mresultat{x \neq -1}. Le calcul de la fonction dérivée donne alors $$ f ' (x) = {-2 \over (x+1)²} + 1 = {-2 + x^2 + 2x + 1 \over (x+1)^2} = \dresultat{{x^2 + x - 1 \over (x+1)^2} = f' (x)} $$ du signe de $x^2 + x - 1$ puisque $(x+1)^2$ est toujours strictement positif si $x \neq -1$. Comme $\Delta = 8 = (2\sqrt2)^2$ est strictement positif, on trouve deux racines réelles $x_1 = -1 - \sqrt2 \simeq -2, 41$ et $x_2 = -1 + \sqrt2 \simeq 0, 41$, et $x^2 + x - 1$ est négatif (signe de $-a$) entre $x_1$ et $x_2$, ce qui donne le tableau de variations suivant~: \medskip \centerline{$$\vbox{ \eightpoint\rm \def \hfq{\hfil \ } \offinterlineskip \halign{ % preamble &\hfq #\hfq \cr $x$& \vrule depth 5pt & $-\infty$&& $x_1$&& $-1$&& $x_2$&& $+\infty$% \cr \noalign{\hrule} $f' (x)$& \vrule height 10pt depth 3pt && $+$& $0$& $-$ & \doublevrule & $-$& $0$& $+$ \cr \noalign{\hrule} \bbuucenter{$f (x)$}& \vrule& &\bbrightuuparrow & \bbuup{$\simeq -5, 83$}& \bbrightddownarrow & \doublevrule & \bbrightddownarrow & \down{$\simeq -0, 17$} & \bbrightuuparrow &% \cr }} $$} \medskip où $f (x_1) = -2\sqrt2 - 3$ et $f (x_2) = 2\sqrt2 - 3$. \itemnum Comme $f (1) = 0$ et que $f' (1) = 1/2$, on trouve pour équation de $\Delta$~: \mresultat{y = {1\over2} (x-1)}. \itemnum \vtop{\eightpoint \rm \halign{ % preamble \tv #&& \cc{$#$}& \tv # \cr \noalign{\hrule} & x&& -{9\over10}&& -{4\over5}&& -{3\over4}&& -{1\over2} && 0&& 1&& 2&& 3&& 4&& 9&& 15& \cr \noalign{\hrule} & f (x)&& 17, 1&& 5, 25&& 7, 2&& 1, 5&& 0&& 0&& 2/3&& 3/2&& 2, 5&& 7, 2&& 13, 125& \cr \noalign{\hrule} }} \def \epspath{% $HOME/tex_doc/lycee/database/1ere/sti/analyse/fonction/} \epsfxsize = 115mm \itemnum $$ \superboxepsillustrate{fct_014.ps} $$ \fincorrige