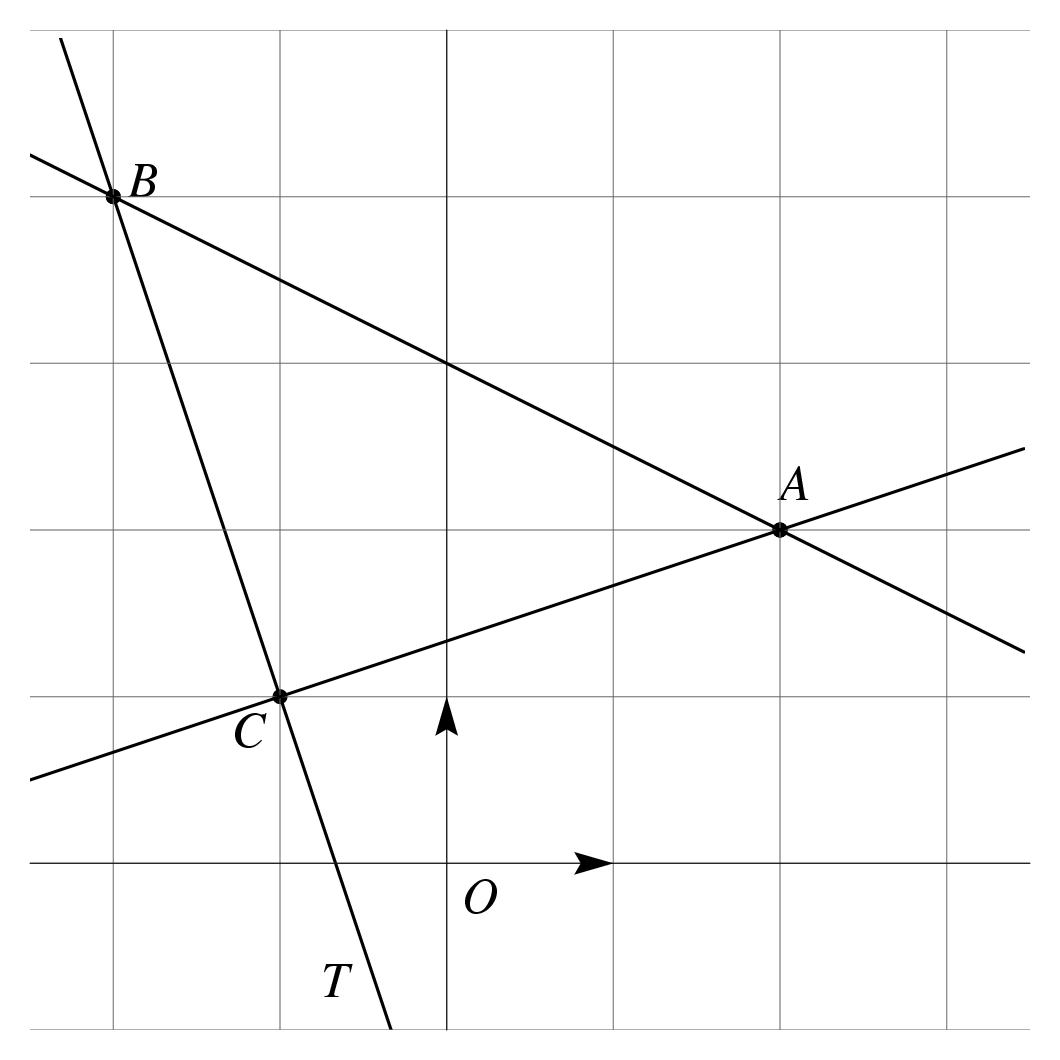
\exo {Géométrie analytique} Dans le plan rapporté à un repère orthonormé $(O, \vec \imath, \vec \jmath\,)$ (unité~: 1~cm ou 1~grand carreau), on considère les points $A (2, 2)$, $B (-2, 4)$ et $C (-1, 1)$. \itemnum Placer les points $A$, $B$ et $C$. \itemnum On considère la droite $T$ d'équation $y = -3x -2$. \itemitemalph Représenter la droite $T$ sur le dessin précédent. \itemitemalph Montrer que le point $C$ est sur la droite $T$. \itemnum Calculer les coordonnées des vecteurs $\overrightarrow{AB}$ et $\overrightarrow{AC}$. En déduire les distances $AB$ et $AC$. \itemitemalphnum Déterminer l'équation réduite de la droite $(AC)$. \itemitemalph Quel est le coefficient directeur de la droite $(BC)$~? \itemnum Que peut-on dire du triangle $ABC$~? \finexo \corrige {} \def \epspath {% $HOME/tex_doc/lycee/database/1ere/sti/geometry/analyt/} \epsfxsize = 80mm \itemnum $$ \superboxepsillustrate {synt_006.ps} $$ \itemnum Le point $C$ a pour coordonnée $C (-1, 1)$, et ses coordonnées vérifient l'équation de la droite $T~: y = -3x - 2$. Donc \tresultat {$C$ est sur la droite $T$}. \itemnum On trouve $$ \overrightarrow {AB} = {x_B - x_A \choose y_B - y_A} \quad {\rm soit} \quad \dresultat {\overrightarrow {AB} = {-4 \choose 2}} \quad {\rm et} \quad \dresultat {\overrightarrow {AC} = {-3 \choose -1}} $$ \item {} Ici, comme $AB = \Vert \overrightarrow {AB}\Vert = \sqrt {(-4)^2 + 2^2}$, il vient $$ \dresultat {AB = \sqrt {20} = 2\sqrt 5} \qquad {\rm et} \qquad \dresultat {AC = \sqrt {10}} $$ \itemalphnum L'équation de la droite $(AC)$ est de la forme $y = ax+b$ où $a$ et $b$ sont deux constantes réelles à déterminer. Des deux conditions \og la droite passe par $A (2, 2)$\fg \ et \og la droite passe par $C$\fg , on tire le système~: $$ \matrix { \scriptstyle (1) \cr \scriptstyle (2) \cr } \cases { 2 = 2a + b \cr 1 = -a + b \cr } \qquad \Longrightarrow \matrix { \scriptstyle (1)-(2) \cr \scriptstyle (2) \cr } \cases { 1 = 3a \cr 1 = -a + b \cr } \qquad {\rm d'où} \qquad \dresultat {(a, b) = \left( {1\over 3}, {4\over 3}\right) } $$ L'équation réduite de la droite $(AC)$ est donc \dresultat {(AC)~: y = {1\over 3} (x+4)}. \itemalph Le vecteur $\displaystyle {\overrightarrow {BC} = {1 \choose -3}}$, donc \tresultat {le coefficient directeur de $(BC)$ est $\displaystyle {-3\over 1} = -3$}. \itemnum On a $BC = \Vert \overrightarrow {BC}\Vert = \sqrt {10}$. Le triangle $ABC$ est donc \tresultat {isocèle} (puisque $AC=BC$), et \tresultat {rectangle en $C$} (par Pythagore puisque $AB^2 = AC^2 + BC^2$). \fincorrige