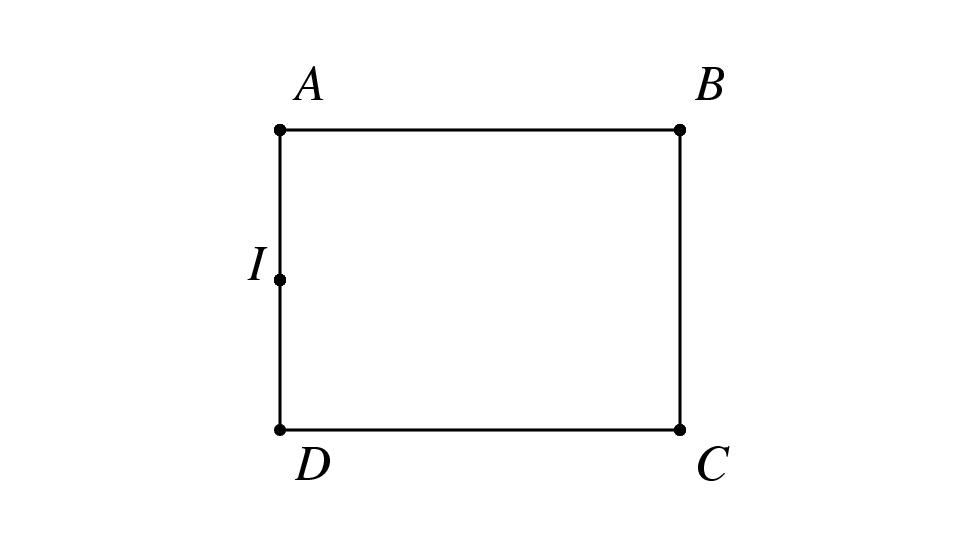
%% format (plain.tex + fichiers de macro) OU (jpv.tex) %% fichiers de macro basejpv.tex + columns.tex + illustr.tex %% sujet equations, inequations, fractions %% date 09-10-97 %% auteur jp vignault \exo{\`A partir d'un dessin} On considère la figure ci-dessous dans le plan rapporté à un repère orthonormé $(O, \vec\imath, \vec \jmath\,)$~: $ABCD$ est un rectangle, $AB=4$, $BC=3$, et $I$ est le milieu du segment $[AD]$. \def \epspath{% $HOME/tex_doc/lycee/database/1ere/sti/geometry/scalaire/} \epsfxsize = 100mm $$ \superboxepsillustrate{scal_014.ps} $$ Déterminer, en expliquant les calculs, les produits scalaires suivants~: \columns 5 \alph\ $\overrightarrow{AB} \cdot \overrightarrow{CD}$ \alph\ $\overrightarrow{AB} \cdot \overrightarrow{CB}$ \alph\ $\overrightarrow{BI} \cdot \overrightarrow{AD}$ \alph\ $\overrightarrow{IB} \cdot \overrightarrow{IC}$ \alph\ $\overrightarrow{CA} \cdot \overrightarrow{DB}$ \endcolumns \finexo \corrige{} \itemalph Comme $\overrightarrow{CD} = - \overrightarrow{AB}$, on a $$ \overrightarrow{AB} \cdot \overrightarrow{CD} = - \overrightarrow{AB} \cdot \overrightarrow{AB} = - \overrightarrow{AB}^2 = \dresultat{-16} $$ \itemalph Comme les vecteur $\overrightarrow{AB}$ et $\overrightarrow{CB}$ sont orthogonaux, on a $$ \dresultat{\overrightarrow{AB} \cdot \overrightarrow{CB} = 0} $$ \itemalph Comme $\overrightarrow{AD} = \overrightarrow{BC}$, on a $$ \overrightarrow{BI} \cdot \overrightarrow{AD} = \overrightarrow{BI} \cdot \overrightarrow{BC} = \overline {BI'} \times \overline {BC} $$ où $I'$ est le projeté orthogonal du point $I$ sur la droite $(BC)$. Le point $I'$ est é\-vi\-dem\-ment le milieu du segment $[BC]$. D'où $$ \overrightarrow{BI} \cdot \overrightarrow{AD} = 3 \times {3 \over 2} \qquad {\rm soit} \qquad \dresultat {\overrightarrow{BI} \cdot \overrightarrow{AD} = {9 \over 2}} $$ \itemalph Pour cette question, il est difficile d'utiliser le théorème de projection. On va donc décomposer. Deux solutions possibles~: $$\eqalign{ \bullet \qquad \overrightarrow{IB} \cdot \overrightarrow{IC} &= \overrightarrow{IB} \cdot \left( \overrightarrow {ID} + \overrightarrow {DC}\right) \cr &= \overrightarrow{IB} \cdot \overrightarrow {ID} + \overrightarrow{IB} \cdot \overrightarrow {DC} \cr &= \overline {IA} \times \overline {ID} + \overline {DC} \times \overline {DC} = -{3\over 2} \times {3\over 2} + 16 = \dresultat {{55 \over 4}} \cr \bullet \qquad \overrightarrow{IB} \cdot \overrightarrow{IC} &= (\overrightarrow{IA} + \overrightarrow{AB}) \cdot (\overrightarrow{ID} + \overrightarrow{DC}) \cr &= \underbrace {\overrightarrow{IA} . \overrightarrow{ID} }_{ -IA^2} + \underbrace {\overrightarrow{IA} . \overrightarrow{DC} }_{ 0} + \underbrace {\overrightarrow{AB} . \overrightarrow{ID} }_{ 0} + \underbrace {\overrightarrow{AB} . \overrightarrow{DC} }_{ AB^2} \cr &= -{9 \over 4} + 16 = \dresultat {{55 \over 4}} }$$ \itemalph Là encore, il faut utiliser la décomposition. Deux exemples de décompositions possibles~: $$ \eqalign { \bullet \qquad \overrightarrow {CA} \cdot \overrightarrow {DB} &= \overrightarrow {CA} \cdot \left( \overrightarrow {DC} + \overrightarrow {CB} \right) \cr &= \overrightarrow {CA} \cdot \overrightarrow {DC} + \overrightarrow {CA} \cdot \overrightarrow {CB} \cr &= \overline {CD} \times \overline {DC} + \overline {CB} \times \overline {CB} = - 16 + 9 = \dresultat{- 7} \cr \bullet \qquad \overrightarrow{CA} \cdot \overrightarrow{DB} &= (\overrightarrow{CD} + \overrightarrow{DA}) \cdot (\overrightarrow{DC} + \overrightarrow{CB}) \cr &= \underbrace {\overrightarrow{CD} . \overrightarrow{DC} }_{ -DC^2} + \underbrace {\overrightarrow{CD} . \overrightarrow{CB} }_{ 0} + \underbrace {\overrightarrow{DA} . \overrightarrow{DC} }_{ 0} + \underbrace {\overrightarrow{DA} . \overrightarrow{CB} }_{ DA^2} \cr &= - 16 + 9 = \dresultat{- 7} \cr } $$ \fincorrige