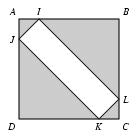
\exo {Bande à part} \def \epspath {% $HOME/tex_doc/lycee/database/2nd/algebre/equations/} \bigskip \rightsuperboxepsillustrate {geom_008.ps}{7} Dans le dessin ci-dessous, $ABCD$ est un carré, et on a $$ AI = AJ = CK = CL = 10\cm . $$ L'aire de la nade blanche est égale à $1\m ^2$. Donner une valeur exacte du côté du carré. {\sl Remarque}~: $1\cm = 0, 01\m $. \finexo \corrige Posons $x$ la longueur inconnue $JD$, et exprimons toutes les quantités en mètres. Les triangles $IBL$ et $KDJ$ sont rectangles isocèles de côté $x$, cependant que les triangles $AIJ$ et $LCK$ sont rectangles isocèles de côté $0, 1$. Le carré $ABCD$ est de côté $x+0, 1$. \def \epspath {% $HOME/tex_doc/lycee/database/2nd/algebre/equations/} $$ \superboxepsillustrate {geom_008a.ps} $$ L'aire du carré $ABCD$ étant égale à la somme des aires de ses parties, il vient $$\displaylines { {\cal A} (ABCD) = {\cal A} (AIJ) + {\cal A} (LCK) + {\cal A} (IBL) + {\cal A} (KDJ) + {\cal A} (IJKL) \cr \Longleftrightarrow \quad (x+0, 1)^2 = {1\over 2} (0, 1)^2 + {1\over 2} (0, 1)^2 + {1\over 2} x^2 + {1\over 2} x^2 + 1 \cr \Longleftrightarrow \quad x^2 + 2 \times 0, 1 \times x + (0, 1)^2 = (0, 1)^2 + x^2 + 1 \cr \Longleftrightarrow \quad 2 \times 0, 1 \times x = 1 \cr \Longleftrightarrow \quad x = {1\over 2 \times 0, 1} = {1\over 2 \times {1\over 10}} = {1\over {2\over 10}} = {10\over 2} = 5 \cr }$$ D'où l'unique solution~: \dresultat {x = 5\m } et le côté du carré est \dresultat {AB = 5, 1\m }. \fincorrige