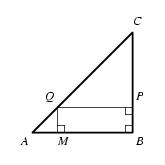
\exo {Aire d'un rectangle variable} \def \epspath {% $HOME/tex_doc/lycee/database/2nd/analyse/fonctions/} Le triangle rectangle isocèle $ABC$ est tel que $AB = BC = 4\cm $. On note $M$ le point de $[AB]$ tel que $AM = x$ avec $0\leq x \leq 4$. $$ \superboxepsillustrate {geom_004.ps} $$ \itemnum Calculer $MB$ en fonction de $x$. \itemnum Montrer que l'aire $S (x)$ du rectangle $MBPQ$ est égale à~: $x (4-x)$. \itemnum Calculer $S(1)$, $S (2)$, $S (3)$. \itemnum Pour quelle valeur de $x$ le rectangle $MBPQ$ est-il un carré~? \itemitemalphnum Vérifier que $S (x) = 4 - (x-2)^2$. \itemitemalph Résoudre alors $S (x) = 3$. \finexo \corrige {} \itemnum On a clairement \dresultat {MB = 4-x}. \itemnum Le triangle $ABC$ est isocèle en $B$, donc $\widehat A = 45^\circ $. De plus, on a $\widehat {AMQ} = 90°$. De part la somme des angles dans le triangle $AMQ$, on en déduit que $\widehat {AQM} = 45°$. \item {} Finalement, le triangle \tresultat {$AMQ$ est isocèle} puisqu'il possède $2$~angles à $45°$. En particulier, on a \dresultat {AM = MQ = x}. \item {} Pour l'aire du rectangle $MBPQ$, il vient finalement $$ S (x) = MB \times MQ \qquad {\rm soit} \qquad \dresultat {S (x) = x (4-x)}. $$ \itemnum On trouve~: \dresultat {S (1) = 3}, \dresultat {S (2) = 4}, \dresultat {S (3) = 3}. \itemnum Si $MBPQ$ est un carré, on a alors $$ MB = MQ \qquad {\rm soit} \qquad x = 4-x \quad \Longleftrightarrow \quad 2x = 4 \quad \Longleftrightarrow \quad \dresultat {x = 2} $$ \itemalphnum Il vient~: $$\eqalign { 4 - (x-2)^2 &= 4 - \big( x^2 - 4x + 4\big) \cr &= 4 - x^2 + 4x - 4 \qquad {\rm soit} \qquad \dresultat {4 - (x-2)^2 = -x^2 + 4x}. \cr }$$ Or $S (x) = x(4-x) = 4x - x^2$. On a donc bien \dresultat {S (x) = 4 - (x-2)^2}. \itemalph Il vient~: $$\eqalign { S (x) = 3 \quad &\Longleftrightarrow \quad 4 - (x-2)^2 = 3 \cr &\Longleftrightarrow \quad 1 - (x-2)^2 = 0 \qquad \hbox {on reconnaît une expression du type $a^2 - b^2$} \cr &\Longleftrightarrow \quad \big( 1 - (x-2)\big) \big( 1 + (x-2)\big) = 0 \cr &\Longleftrightarrow \quad (3 - x) (x-1) = 0 \cr &\Longleftrightarrow \quad 3 - x = 0 \qquad {\rm ou} \qquad x-1 = 0 \cr }$$ D'où les deux solutions~: \tresultat {$x = 1$ et $x = 3$}. \fincorrige